Скорость – это величина, которая описывает изменение положения объекта со временем. Однако, в физике существуют также понятия проекции скорости, которые позволяют разделить вектор скорости на составляющие, отвечающие за его движение вдоль разных осей.
Проекция скорости является важным инструментом в физике, так как позволяет анализировать движение объектов в различных направлениях и находить его характеристики. Важно понимать, что проекции скорости всегда имеют знаки, которые указывают на направление движения объекта.
Знак проекции скорости может быть положительным или отрицательным. Если проекция скорости положительна, это означает, что объект движется вперед по данной оси. Если же проекция скорости отрицательна, это говорит о движении объекта в противоположном направлении. Отличить положительную и отрицательную проекцию скорости можно по знакам перед числами величин скорости.
Основные понятия физической проекции скорости
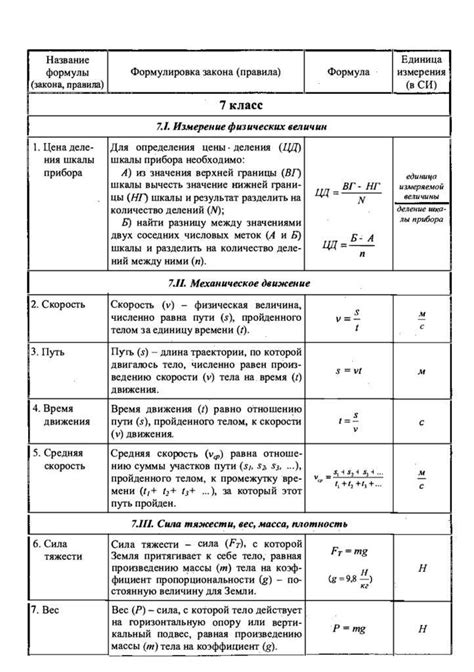
Одним из основных понятий в физической проекции скорости является векторная проекция. Векторная проекция скорости определяется как длина вектора проекции, равная произведению длины вектора скорости на косинус угла между этим вектором и осью или плоскостью, вдоль которых происходит проекция.
Другим важным понятием является скалярная проекция скорости. Скалярная проекция скорости рассчитывается как произведение длины вектора скорости на косинус угла между этим вектором и осью или плоскостью проекции. Отличие от векторной проекции заключается в том, что скалярная проекция скорости является численной величиной.
Проекция скорости играет важную роль в решении различных физических задач. Например, при движении тела под углом к горизонту, для вычисления его горизонтальной и вертикальной составляющей скорости необходимо провести проекцию скорости на соответствующие оси.
Важно понимать, что проекция скорости зависит от выбранной системы координат и может изменяться при изменении этой системы. Поэтому в физике необходимо правильно выбирать систему координат для проведения проекции скорости и анализа движения тела.
Проекция скорости: определение и сущность
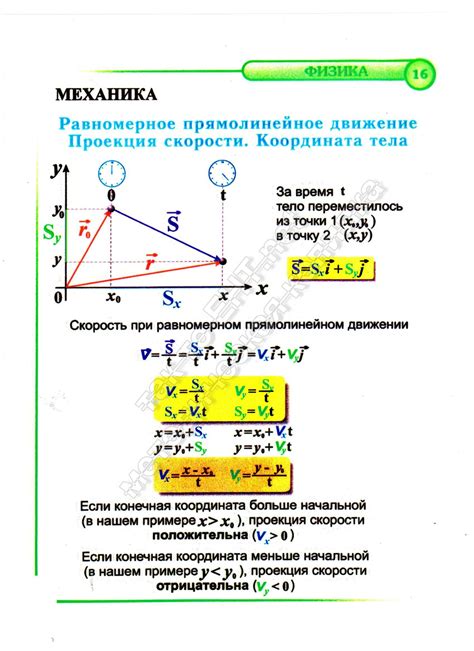
Для определения проекции скорости необходимо знать направление вектора скорости и угол между этим направлением и выбранным направлением проекции. Проекция скорости может быть положительной или отрицательной, в зависимости от угла между направлениями.
Проекция скорости имеет важное значение при решении задач динамики, так как позволяет учитывать только составляющую скорости в нужном направлении и упрощает анализ движения объекта. Она позволяет разделить вектор скорости на две составляющие: горизонтальную и вертикальную.
Для наглядного представления проекции скорости можно использовать таблицу, в которой указываются значения векторов скорости и их проекций по направлениям. Такая таблица помогает увидеть зависимость между векторами скорости и их проекциями на координатные оси.
| Направление | Вектор скорости | Проекция скорости |
|---|---|---|
| Горизонтальное | Vx | Vx |
| Вертикальное | Vy | Vy |
Таким образом, проекция скорости играет важную роль в физике и позволяет разбить вектор скорости на составляющие, что упрощает анализ и решение задач динамики.
Как рассчитать проекцию скорости по вектору скорости?
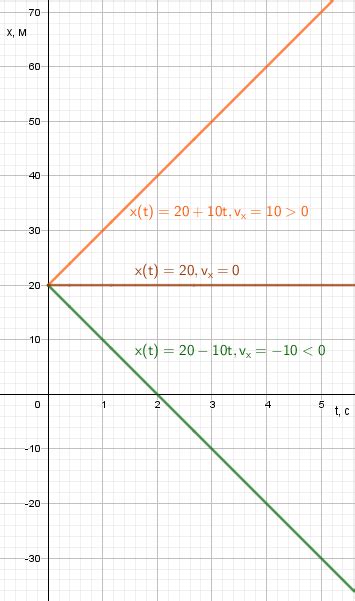
Для расчета проекции скорости по вектору скорости необходимо использовать математические методы векторной алгебры. Сначала необходимо разложить вектор скорости на две составляющие: горизонтальную и вертикальную.
Для этого нужно знать угол между вектором скорости и вектором направления, по которому необходимо рассчитать проекцию. Затем, используя формулы тригонометрии, можно найти значения проекции скорости.
Для горизонтальной проекции скорости можно использовать следующую формулу:
𝕃х = 𝕃 * cos(α)
где:
- 𝕃х – горизонтальная проекция скорости;
- 𝕃 – вектор скорости;
- α – угол между вектором скорости и вектором направления.
Аналогично, для вертикальной проекции скорости используется формула:
𝕃у = 𝕃 * sin(α)
где:
- 𝕃у – вертикальная проекция скорости.
Таким образом, зная значения вектора скорости и угол между вектором скорости и вектором направления, можно рассчитать проекцию скорости вдоль выбранного направления.
Основные принципы проекции скорости
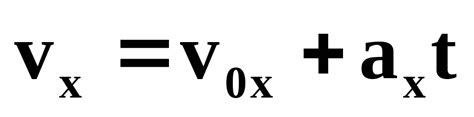
Одним из основных принципов проекции скорости является то, что проекция скорости вдоль оси координат всегда меньше или равна абсолютной величине самой скорости. Другими словами, скорость тела состоит из двух компонент: одна компонента направлена вдоль оси, а другая - перпендикулярна ей.
Еще одним принципом проекции скорости является то, что проекции скорости двух тел, движущихся в одном направлении, можно складывать. Таким образом можно определить общую проекцию скорости системы тел.
Проекция скорости может быть положительной или отрицательной в зависимости от направления движения тела. Если проекция скорости направлена в положительном направлении оси, то значение проекции скорости положительное. Если проекция скорости направлена в отрицательном направлении оси, то значение проекции скорости отрицательное.
Проекция скорости также может использоваться для определения пути, пройденного телом. Для этого необходимо умножить проекцию скорости на время движения тела. Таким образом можно определить расстояние, которое пройдет тело за определенное время.
Примеры задач по проекции скорости в физике

- Задача №1: Машина движется по прямой и имеет скорость 50 км/ч. Найти проекцию скорости на ось X (горизонтальную) и ось Y (вертикальную), если угол между направлением движения и осью X составляет 30°.
- Задача №2: Мяч брошен под углом 45° к горизонту со скоростью 20 м/с. Найти проекцию скорости на горизонтальную ось и вертикальную ось в момент броска.
- Задача №3: Автомобиль движется по окружности радиусом 100 м со скоростью 10 м/с. Каковы проекции скорости на оси X и Y в произвольный момент времени?
Решение: Для нахождения проекций скорости на оси X и Y воспользуемся тригонометрическими соотношениями. Проекция скорости на ось X равна Vx = V * cos(θ), где V – абсолютная величина скорости, а θ – угол между направлением скорости и осью X. В нашем случае V = 50 км/ч, θ = 30°. Подставляем значения: Vx = 50 * cos(30°) = 50 * √3/2 ≈ 43.3 км/ч. Аналогично, проекция скорости на ось Y равна Vy = V * sin(θ). Подставляем значения: Vy = 50 * sin(30°) = 50 * 1/2 = 25 км/ч. Таким образом, проекции скорости на оси X и Y составляют примерно 43.3 км/ч и 25 км/ч соответственно.
Решение: В данной задаче также воспользуемся тригонометрическими соотношениями. Проекция скорости на горизонтальную ось (ось X) в момент броска равна Vx = V * cos(θ), где V – абсолютная величина скорости, а θ – угол между направлением скорости и осью X. В нашем случае V = 20 м/с, θ = 45°. Подставляем значения: Vx = 20 * cos(45°) = 20 * √2/2 = 10 * √2 м/с. Аналогично, проекция скорости на вертикальную ось (ось Y) в момент броска равна Vy = V * sin(θ). Подставляем значения: Vy = 20 * sin(45°) = 20 * √2/2 = 10 * √2 м/с. Таким образом, проекции скорости на горизонтальную ось и вертикальную ось в момент броска составляют 10 * √2 м/с каждая.
Решение: В данной задаче проекции скорости на оси X и Y будут меняться по мере движения автомобиля по окружности. В произвольный момент времени проекция скорости на ось X равна Vx = V * cos(θ), где V – абсолютная величина скорости, а θ – угол между направлением скорости и осью X. Угол θ в данной задаче может быть найден с помощью геометрии и равен θ = arcsin(R/Rt), где R – радиус окружности, Rt – абсолютная величина радиус-вектора автомобиля в данном моменте времени. Подставляем значения: Vx = 10 * cos(arcsin(100/Rt)). Аналогично, проекция скорости на ось Y равна Vy = V * sin(θ), где θ = arcsin(R/Rt). Подставляем значения: Vy = 10 * sin(arcsin(100/Rt)). Таким образом, проекции скорости на оси X и Y будут меняться в зависимости от радиуса-вектора автомобиля в каждый момент времени.
Это лишь некоторые примеры задач, связанных с проекциями скорости в физике. Решение таких задач поможет разобраться с основными концепциями и применением проекций скорости в различных ситуациях.
Значение проекции скорости в практической физике

В практической физике значения проекции скорости помогают решать такие важные задачи, как вычисление времени полета объекта, определение дальности полета, оценка максимальной высоты подъема и траектории движения.
Примером практического использования проекции скорости может служить выстрел из пневматической винтовки. Проекция начальной скорости пули на горизонтальное направление позволяет определить, на каком расстоянии от пушки пуля попадет в цель. Расчет проекции скорости также позволяет определить, на какую высоту поднимется пуля и на каком расстоянии она достигнет максимального подъема.
Значение проекции скорости также играет важную роль в механике автомобилей. Зная проекцию скорости автомобиля на горизонтальную ось, можно рассчитать пройденное расстояние за определенный промежуток времени и вычислить среднюю скорость движения. Проекция скорости также используется для определения максимальной скорости автомобиля в зависимости от различных факторов, таких как уклон дороги или сопротивление воздуха.
Таким образом, значение проекции скорости в практической физике заключается в умении определить скорость и траекторию движения объекта, а также решить различные задачи, связанные с движением объектов в пространстве.



