Равнобедренный треугольник является особым типом треугольника, у которого две стороны равны. Следовательно, углы при основании такого треугольника также равны, а величина каждого из них составляет половину суммы углов при основании. Таким образом, в равнобедренном треугольнике существует угол, который называется углом при основании, и остальные два угла равны.
Один из способов нахождения тангенса угла в равнобедренном треугольнике - использование определения тангенса как отношения противолежащего и прилежащего катетов прямоугольного треугольника. В равнобедренном треугольнике противолежащий катет одновременно является основанием треугольника, а прилежащий катет - это равная боковая сторона треугольника. Таким образом, тангенс угла в равнобедренном треугольнике равен отношению половины основания к равной боковой стороне.
Если обозначить одну из равных сторон равнобедренного треугольника как a, а угол при основании как α, то получим, что тангенс угла α равен отношению половины основания к равной стороне: tg(α) = a/2a = 1/2. Таким образом, тангенс угла в равнобедренном треугольнике всегда равен 1/2.
Тангенс: определение и свойства
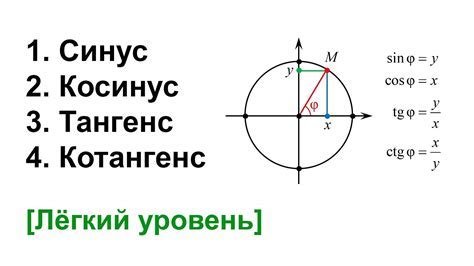
Тангенс угла обозначается сокращенно как tg и определяется как отношение сторон прямоугольного треугольника: tg α = a/b, где α – угол, a – противолежащий катет, b – прилежащий катет.
Основные свойства тангенса:
- Значение тангенса всегда является вещественным числом;
- Тангенс является периодической функцией с периодом π (или 180°), что означает, что tg(α + π) = tg α;
- Функция тангенса является нечётной функцией, что означает tg(–α) = –tg α.
Важно помнить, что для значений угла α, при которых прилежащий катет равен нулю (b = 0), функция тангенса tg α неопределена.
Равнобедренный треугольник: определение и свойства
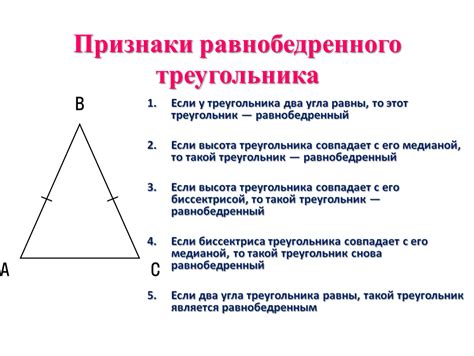
Определение равнобедренного треугольника можно выразить следующей формулой: a = c, где a и c - равные стороны треугольника, b - основание.
Свойства равнобедренного треугольника:
- Основание треугольника (сторона b) является средней линией по отношению к равным сторонам (сторонам a и c).
- Углы при основании (углы между стороной b и равными сторонами) равны между собой и называются углами при основании.
- Угол, образованный равными сторонами (угол между сторонами a и c), называется вершинным углом или углом при вершине.
- Сумма углов равнобедренного треугольника равна 180 градусов.
- Тангенс угла при основании равен отношению половины основания к высоте.
Таким образом, равнобедренные треугольники являются особой геометрической фигурой, имеющей несколько характерных свойств, которые могут быть использованы для решения различных задач в геометрии и тригонометрии.
Тангенс угла в равнобедренном треугольнике

В равнобедренном треугольнике две стороны при основании равны между собой. Такой треугольник имеет несколько особых свойств, включая равенство некоторых углов.
Угол при основании равнобедренного треугольника делит его на два прямоугольных треугольника. Тангенс угла в равнобедренном треугольнике можно выразить через соотношение длины катета и гипотенузы.
Тангенс угла в равнобедренном треугольнике равен отношению длины катета (боковой стороны при основании) к половине длины основания (или половине длины гипотенузы).
Формула для вычисления тангенса угла в равнобедренном треугольнике:
tan(A) = a / (b / 2)
где: tan(A) - тангенс угла А, a - длина катета (боковой стороны при основании), b - длина основания (или гипотенузы).
Например, если основание равнобедренного треугольника имеет длину 10 единиц, а катет 8 единиц, то тангенс угла будет равен 8 / (10 / 2) = 8 / 5 = 1.6.
Тангенс угла в равнобедренном треугольнике является одним из параметров, которые можно использовать для вычисления других значений угла или сторон треугольника.
Примеры вычисления тангенса угла в равнобедренном треугольнике
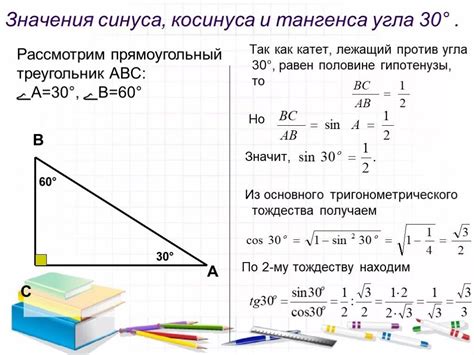
Для вычисления тангенса угла в равнобедренном треугольнике можно воспользоваться следующей формулой:
tg(angle) = (lenght_of_base/2) / altitude_to_base
Давайте рассмотрим примеры:
Пример 1:
У нас есть равнобедренный треугольник с длиной основания 10 и высотой, опущенной на основание, равной 8. Найдем тангенс угла:
tg(angle) = (10/2) / 8 = 5/8 = 0.625
Пример 2:
Допустим, у нас есть равнобедренный треугольник с основанием, равным 6, и высотой, равной 4. Найдем значение тангенса угла:
tg(angle) = (6/2) / 4 = 3/4 = 0.75
Таким образом, мы можем вычислить тангенс угла в равнобедренном треугольнике, используя соответствующую формулу. Это позволяет нам определить величину угла и применить ее в различных математических задачах.
Практическое применение тангенса угла в равнобедренном треугольнике

Триангуляция – это метод определения высоты объекта, который основан на измерении углов. Если известно, что треугольник на местности является равнобедренным, можно использовать тангенс для нахождения высоты объекта. Для этого необходимо измерить два угла треугольника и расстояние между ними. Затем, используя формулу расчета тангенса угла в равнобедренном треугольнике, можно вычислить высоту объекта.
Практические примеры применения тангенса угла в равнобедренном треугольнике есть не только в геодезии и топографии. Например, в архитектуре он используется для расчета высоты строений и составления графиков наклона крыш, что помогает сделать строение более устойчивым.
Еще одним практическим применением тангенса угла в равнобедренном треугольнике является сфера образования. В геометрии этот тригонометрический коэффициент используется для нахождения высоты и длины сторон треугольника. Тангенс также имеет важное значение в физике, так как позволяет рассчитывать силу трения, механические колебания и другие механические величины.
Кроме того, тангенс угла в равнобедренном треугольнике имеет применение в информационных технологиях. В компьютерной графике и визуализации он используется для рендеринга трехмерных объектов и текстур, а также для нахождения точек пересечения линий и плоскостей.



