Математика - это фундаментальная наука, которая позволяет нам понять, описывать и решать разнообразные математические задачи. В процессе изучения математики, мы сталкиваемся с различными математическими символами, которые помогают нам описывать и передавать информацию более точно и компактно. Один из таких символов - знак трех точек (...), который имеет свое собственное значение в математике.
Знак трех точек в математике обозначает пропущенные элементы в последовательности или множестве. Он подобен многоточию в литературе, которое указывает на продолжение неопределенности или неполноты. Знак трех точек часто используется в задачах, которые требуют нам найти пропущенный элемент или продолжить последовательность.
Например, если дана последовательность чисел 1, 3, 5, ..., то трех точек (...) можно использовать, чтобы указать на необходимость продолжения последовательности. Таким образом, можно сказать, что данная последовательность состоит из нечетных чисел, начиная с 1, и элементы между ними пропущены. Знак трех точек помогает нам сделать такое заключение и более точно описать последовательность чисел.
Помимо этого, знак трех точек также используется в математическом анализе и теории множеств для обозначения бесконечной последовательности или множества. Например, множество натуральных чисел можно записать как N = {1, 2, 3, ...}, где трех точек указывают на то, что последовательность чисел продолжается бесконечно. Этот знак помогает нам представить бесконечные множества и последовательности в компактной и лаконичной форме.
Понятие и история происхождения и распространения

Знак трех точек, известный также как "многоточие" или "эллипсис", представляет собой математическую нотацию, используемую для обозначения продолжения последовательности или серии в некотором образе. Он состоит из трех точек, расположенных в горизонтальной линии.
Исторически понятие многоточия появилось в древнегреческих математических текстах, где использовался как символ бесконечности. В дальнейшем он нашел свое применение в различных областях математики, физики и информатики.
В математике знак трех точек часто используется для обозначения продолжения последовательности чисел или символов. Например, если у нас есть последовательность чисел 1, 2, 3, ..., мы можем записать ее как 1, 2, 3, ..., n, где n - индекс последнего числа в последовательности.
Также многоточие может использоваться для обозначения пропущенных частей определенного выражения или текста. Например, в алгебре можно записать общую формулу для суммы арифметической прогрессии как S = a + (a + d) + (a + 2d) + ... + (a + (n-1)d), где a - первый член прогрессии, d - разность прогрессии, n - количество членов в прогрессии. В этом случае многоточие указывает на продолжение последовательности слагаемых.
Использование многоточия распространилось также за пределы математики и нашло свое применение в технической и научной литературе, а также в различных формах письменной коммуникации, включая электронные сообщения и интернет-чаты. Оно часто используется для сокращения текста и вызова внимания к фрагменту, которому не уделяется прямое внимание.
Математическая запись: Виды записи и нотация

Одной из основных задач математической записи является представление сложных математических формул, выражений и уравнений в понятной и компактной форме. Ведь часто математические объекты имеют очень большую сложность и размер.
Существует несколько видов записи и нотации в математике:
- Стандартная математическая нотация – это форма записи, которая признана и принята среди математиков во всем мире. Она определяет правила и соглашения, которые должны соблюдаться при записи математических выражений и уравнений. Примеры такой нотации – использование знаков операций (+, -, ×, ÷), знаков сравнения (=, ≠, <, >) и т.д.
- Алгебраическая нотация – это специальная форма записи, которая используется в алгебре для представления алгебраических выражений и уравнений. Здесь используются заглавные и прописные буквы для обозначения переменных и констант, а также знаки операций и другие математические символы.
- Графическая нотация – это форма записи, которая используется для визуального представления математических объектов и отношений. Примеры такой нотации – графы, диаграммы, графики функций и т.д. Графическая нотация позволяет наглядно представить сложные математические конструкции и упрощает их понимание.
Все эти виды записи и нотации взаимосвязаны и дополняют друг друга. Они позволяют математикам представлять, изучать, анализировать и решать задачи в различных областях математики.
Функциональное значение операции над множествами
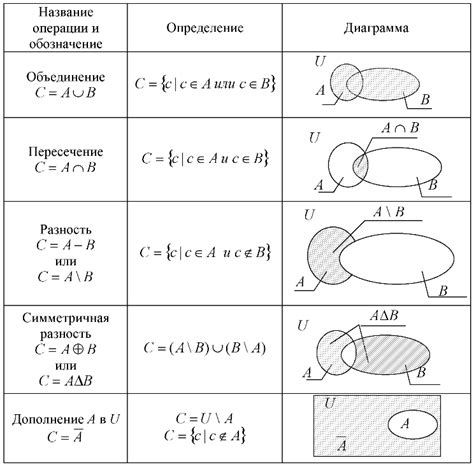
Например, если у нас есть множество A = {1, 2} и множество B = {2, 3}, то их объединение A ∪ B будет равно множеству {1, 2, 3}.
Объединение множеств полезно во многих областях математики и информатики. Например, оно используется при работе с базами данных, когда нужно объединить результаты нескольких запросов. Также операция объединения позволяет решать задачи комбинаторики и теории вероятностей.
Важно отметить, что операция объединения имеет ряд свойств, которые делают ее удобной в использовании. Например, она ассоциативна и коммутативна. Это значит, что порядок объединения множеств не влияет на результат, а также что множества можно объединять поэлементно в любом порядке.
Таким образом, операция объединения с помощью знака трех точек имеет важное функциональное значение в математике и других областях науки.
Примеры использования знака трех точек

- Определение бесконечной суммы: S = a + b + c + ...
- Обозначение обобщения в математической последовательности: x1, x2, x3, ... , xn
- Использование в сокращении описания диапазона значений: x ∈ [1, 10]
- Показ символа с неполным последовательным списком элементов: a, b, c, ..., z
- Указание на продолжение или незавершенность выражения: f(x) = x2 + 2x + ...
- Обозначение пропущенных или упрощенных частей формулы: (a + b + ...) = (x + y + ...)
Особенности использования Контекст и окружение

В математике знаки трех точек (...) часто используются для обозначения неопределенной последовательности чисел или выражений.
Контекст и окружение играют важную роль при интерпретации знака трех точек. Это связано с тем, что знак трех точек может иметь различные значения в разных контекстах.
В математических выражениях знак трех точек может означать продолжение или продолжительность, указывая на то, что последовательность чисел или выражений не является конечной и может быть расширена или продолжена.
В некоторых случаях знак трех точек может также использоваться для обозначения обобщенных или неопределенных значений в задачах или уравнениях. В таком контексте он указывает на то, что существует бесконечное количество возможных значений, соответствующих заданным условиям.
Основное значение знака трех точек в математике заключается в создании гибких выражений, которые позволяют указывать на неопределенность или возможность продолжения. Использование контекста и окружения позволяет более точно определить значение знака трех точек в каждом конкретном случае.



