В геометрии отрезок - это участок прямой, ограниченный двумя точками. Но что означают граничные точки этого отрезка? Граничные точки - это точки, которые лежат на самом отрезке и определяют его концы. Они являются важными элементами геометрических фигур и имеют свои особенности.
Граничная точка отрезка может быть как внутренней, так и внешней. Внутренняя граничная точка лежит внутри отрезка и не является его концом, а внешняя граничная точка лежит за пределами отрезка и также не является его концом. Граничные точки помогают нам формулировать и доказывать различные утверждения о геометрических объектах.
Граничные точки отрезка могут быть одинаковыми, если отрезок является вырожденным, то есть его длина равна нулю. В этом случае граничная точка является единственной точкой, определяющей отрезок. Однако, если отрезок невырожденный, то его граничные точки различны и несовпадающие.
Граничные точки отрезка и их роль в геометрии
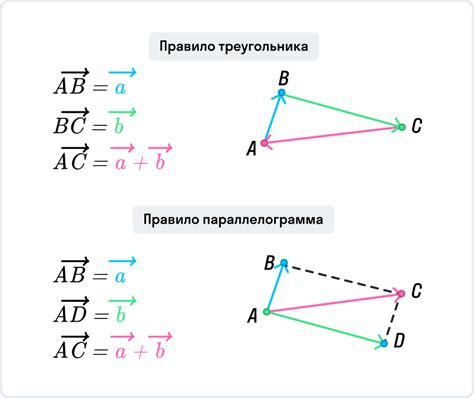
Граничные точки отрезка могут быть представлены как концы отрезка, то есть те точки, которые являются его начальной и конечной точками. Например, если рассматривается отрезок AB, то точки A и B будут его граничными точками.
Граничные точки отрезка служат основой для определения свойств и характеристик самого отрезка. Например, по наличию граничных точек можно определить его длину, положение на числовой прямой и отношение к другим отрезкам.
Граничные точки отрезка также играют важную роль при определении примитивных геометрических фигур, таких как линия, отрезок, полупрямая или прямая. Они помогают визуализировать и понять границы и форму этих фигур.
Помимо этого, граничные точки отрезка могут использоваться при доказательстве теорем и вычислении различных геометрических величин. Например, при доказательстве теоремы о существовании и единственности прямой, проходящей через две различные точки, используются граничные точки отрезка.
Таким образом, граничные точки отрезка являются важными элементами геометрии, которые определяют его свойства и позволяют проводить различные аналитические и геометрические исследования.
Определение граничных точек отрезка
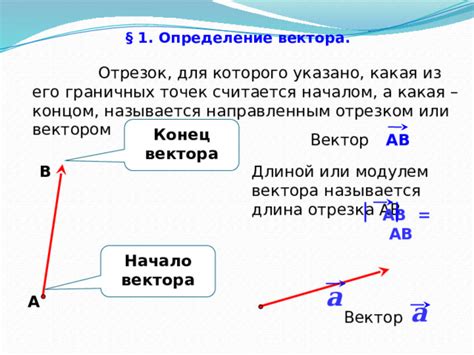
Для определения граничных точек отрезка необходимо знать две базовые характеристики самого отрезка – его начальную и конечную точку.
Начальная точка отрезка – это точка, с которой начинается отрезок, а конечная точка – это точка, на которой отрезок заканчивается. Именно эти две точки образуют границы отрезка и называются граничными точками отрезка.
Граничные точки отрезка обладают особенностью – каждая из них является внутренней точкой для отрезка и внешней точкой для самой прямой, на которой он лежит. Кроме того, граничные точки отрезка могут быть использованы для построения других отрезков или отображения отрезков на координатной плоскости.
| Отрезок | Начальная точка | Конечная точка | Граничные точки |
|---|---|---|---|
| AB | A | B | A, B |
В таблице приведен пример отрезка AB с его начальной точкой A и конечной точкой B. В данном случае граничными точками являются точка A и точка B.
Таким образом, граничные точки отрезка – это две точки, которые образуют его концы и являются его границами.
Роль и значение граничных точек в геометрии

Граничные точки отрезка в геометрии играют важную роль и несут значительное значение. Они определяются как точки, находящиеся на самом краю отрезка и являющиеся его конечными точками. Граничные точки отрезка могут быть указаны как начальная или конечная точка, или же в виде пределов отрезка.
Граничные точки имеют ряд важных свойств и характеристик:
- Они определяют концы отрезка и помогают установить его длину;
- Граничные точки могут быть включены в другие геометрические фигуры, такие как отрезки, отрезки прямой, окружности и другие;
- Они также могут использоваться для определения свойств исходного отрезка, например, его положения или направления.
Главное значение граничных точек состоит в том, что они помогают определить границы и характеристики отрезка в геометрии. Без них, понятие отрезка и его свойства были бы более абстрактными и трудно определяемыми.
Свойства и особенности граничных точек отрезка
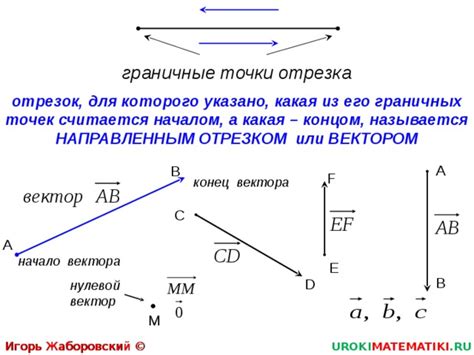
- Граничные точки отрезка лежат на самом отрезке и являются его крайними точками.
- Граничные точки отрезка также являются граничными точками для всех подотрезков данного отрезка.
- Отрезок может иметь одну, две или даже бесконечное количество граничных точек.
- Точка может быть граничной для одного отрезка и внутренней для другого, в зависимости от контекста.
- Граничные точки отрезка разделяют его на две части: левую и правую.
- Левая часть отрезка состоит из всех точек, лежащих слева от граничных точек, включая эти точки.
- Правая часть отрезка состоит из всех точек, лежащих справа от граничных точек, включая эти точки.
Из вышеперечисленных свойств видно, что граничные точки отрезка играют важную роль при рассмотрении отрезков в геометрии. Они определяют его границы и позволяют проводить различные операции с отрезками, такие как деление на подотрезки, определение взаимного положения отрезков и другие. Поэтому понимание свойств и особенностей граничных точек отрезка имеет важное значение при изучении геометрии.
Примеры использования граничных точек в геометрии
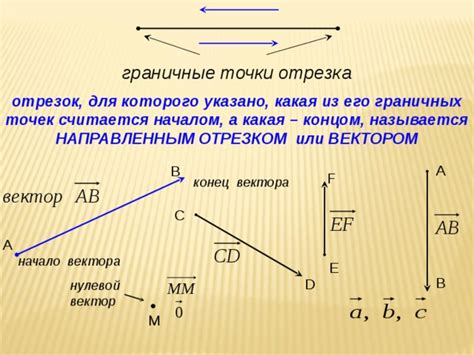
Граничные точки отрезка в геометрии играют важную роль и находят свое применение в различных областях. Рассмотрим несколько примеров использования граничных точек:
1. Интерполяция значений
Граничные точки отрезка могут быть использованы для интерполяции значений между двумя данными. Например, если у нас есть две известные точки на оси координат, то мы можем использовать эти точки, чтобы найти значение в промежуточной точке на отрезке между ними. Это может быть полезно при нахождении промежуточных значений в различных задачах, таких как графики, анимации и численные методы.
2. Нахождение границ областей
Граничные точки также используются для определения границ областей на плоскости. Например, в задачах, связанных с нахождением площади фигур, таких как треугольники, прямоугольники и окружности, граничные точки помогают определить конечные точки фигуры и ее границы.
3. Определение условий равенства и неравенства
Граничные точки также используются в определении условий равенства и неравенства в геометрии. Например, при сравнении значений двух точек на оси координат, граничные точки позволяют установить, когда значения равны или неравны друг другу. Это может быть полезно в задачах сравнения данных или определении отрезков на оси.
Это лишь несколько примеров, и граничные точки могут быть использованы во многих других сферах геометрии. Их значение состоит в том, что они помогают определить границы, интерполировать значения и устанавливать условия равенства и неравенства, что делает их важными инструментами для изучения и применения геометрии.



