Классический метод деления - один из основных алгоритмов в математике, который используется для нахождения частного и остатка от деления двух чисел. Величина остатка при делении зависит от выбранной системы счисления и базы, в которой производится деление.
Однако существуют альтернативные методы, которые способны упростить вычисления. Один из таких методов - схема Горнера. Он используется для деления чисел с фиксированной точностью представления и позволяет ускорить процесс вычисления деления.
Суть схемы Горнера заключается в следующем: вместо того чтобы делить число на базу системы счисления, мы умножаем его на коэффициент, который вычитается из исходного числа, полученного на предыдущем шаге. Таким образом, мы постепенно приближаемся к результату и уменьшаем количество операций деления.
Доказательство числа а для схемы Горнера является нетривиальной задачей. Однако, с помощью математической индукции и арифметических преобразований, можно показать, что результат деления при использовании схемы Горнера будет равен результату деления по классическому методу.
Что такое схема Горнера и как она используется для деления?
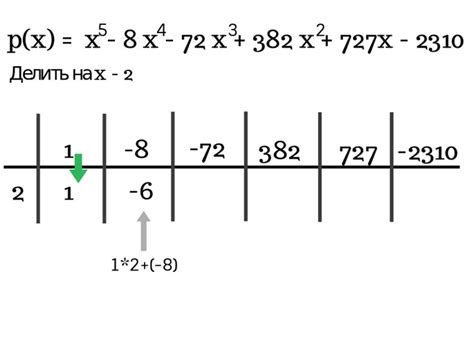
Основная идея схемы Горнера состоит в том, чтобы представить многочлен в виде суммы членов, где каждый член умножается на множитель и складывается с предыдущим результатом. Это позволяет сократить количество операций умножения и сложения, что делает процесс деления более эффективным.
Для использования схемы Горнера для деления необходимо представить многочлен в виде таблицы, где в первом столбце располагаются коэффициенты многочлена, а во втором столбце - значения, полученные при вычислении остатков от деления.
| Коэффициенты | Значения (остатки) |
|---|---|
| a0 | a0 |
| a1 | a0 + a1*x |
| a2 | a0 + a1*x + a2*x2 |
| a3 | a0 + a1*x + a2*x2 + a3*x3 |
Процесс деления с использованием схемы Горнера заключается в последовательном вычислении значений (остатков) исходного многочлена. Результатом деления является последний остаток.
Схема Горнера предоставляет простой и эффективный метод для деления многочленов. Этот метод широко применяется в математике, алгебре и научных исследованиях, где требуется быстрое и точное деление многочленов.
Проблемы классического способа деления и почему требуется замена
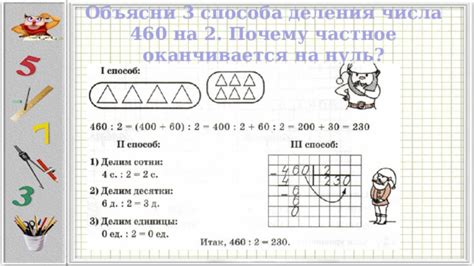
Одной из основных проблем классического способа деления является его сложность и трудоемкость. При делении многочленов или больших чисел, этот метод может требовать значительного количества времени и ресурсов. В результате, решение задач может затягиваться и стать неэффективным.
Еще одной проблемой классического способа деления является его ограниченность в случае нецелочисленных делений. Классический метод применим только для целых чисел и не может быть использован для десятичных или неполных чисел. Это создает неудобства и требует использования дополнительных алгоритмов для решения таких задач.
Схема Горнера является улучшенным методом деления, который позволяет решать задачи более эффективно и универсально. Этот метод основан на использовании многочленов и позволяет работать с большими числами, включая десятичные и неполные дроби.
Таким образом, замена классического способа деления на схему Горнера необходима для улучшения эффективности и универсальности решения математических задач. Она позволяет сократить время и ресурсы, а также работать с разнообразными типами чисел, повышая точность и гибкость метода.
В чем состоит новый способ деления на схему Горнера?

Новый способ деления на схему Горнера основан на использовании группировки слагаемых многочлена, что позволяет уменьшить количество операций умножения и сложения. В результате, время выполнения деления сокращается, что особенно важно при работе с большими многочленами и высокими степенями.
Основная идея нового способа заключается в разделении многочлена на группы слагаемых, каждая из которых имеет свою степень. Затем происходит последовательное вычисление значений групп, при этом значения ранее вычисленных групп многократно используются. Благодаря этому подходу, можно избежать повторного вычисления слагаемых, что значительно ускоряет выполнение операции деления.
Кроме того, новый способ деления на схему Горнера позволяет более эффективно использовать параллельные вычисления, что открывает возможности для ускорения вычислений на многоядерных процессорах и суперкомпьютерах.
Таким образом, новый способ деления на схему Горнера представляет собой инновационный подход к вычислениям многочленов, который значительно повышает эффективность операции деления и открывает новые возможности для параллельных вычислений.
Доказательство числа а на примере схемы Горнера
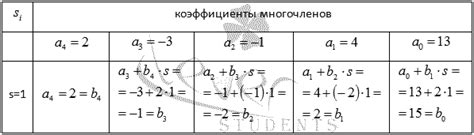
Задача доказать число а заключается в том, чтобы подставить его в схему Горнера и проверить, что полученный результат равен нулю.
Шаг 1: Запишем заданный многочлен в схему Горнера:
P(x) = anxn + an-1xn-1 + ... + a1x + a0
Шаг 2: Делим первый член многочлена P(x) на число а: an / a.
Шаг 3: Домножаем полученное частное на x и прибавляем следующий член многочлена: (an / a)x + an-1.
Шаг 4: Продолжаем этот процесс до последнего члена многочлена.
Шаг 5: Если последний полученный результат равен нулю, то число а является корнем многочлена. Иначе, его можно отбросить в качестве корня.
Таким образом, используя схему Горнера, можно эффективно доказать число а и определить, является ли оно корнем заданного многочлена.
Как работает схема Горнера в применении к делению?
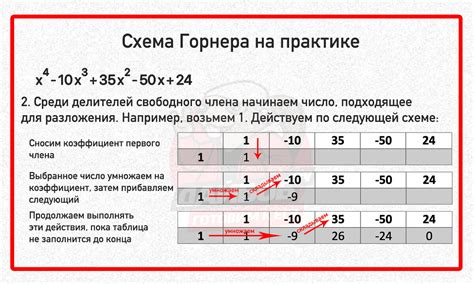
Для применения схемы Горнера к делению многочлена на линейный множитель нужно следовать следующим шагам:
- Записать многочлен в общей форме, где коэффициенты упорядочены по убыванию степеней переменной.
- Найти значение переменной, при котором происходит деление многочлена на линейный множитель. Это значение называется "a".
- Выполнить первый шаг вычисления: умножить старший коэффициент многочлена на "a" и записать результат.
- Проследить схему Горнера, последовательно умножая результаты предыдущего шага на "a" и складывая их с соответствующими коэффициентами многочлена. Полученный результат записывать последовательно.
- После окончания шагов схемы Горнера, последний результат будет являться остатком от деления исходного многочлена на заданный линейный множитель.
Схема Горнера позволяет существенно упростить вычисления и сделать их более быстрыми. Она находит применение не только в математике, но и в других областях, таких как компьютерная графика, криптография, анализ данных и др. Понимание принципа работы схемы Горнера позволяет эффективно использовать ее в решении разнообразных задач.
Преимущества схемы Горнера по сравнению с классическим делением
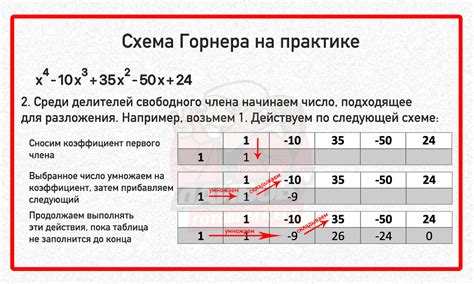
Схема Горнера представляет собой более эффективный и удобный способ деления многочленов, чем классический метод. В классическом делении необходимо выполнить множество операций умножения и вычитания, что может быть трудоемким и затратным процессом. Схема Горнера позволяет значительно упростить процесс деления, сокращая количество операций.
Основное преимущество схемы Горнера заключается в том, что она позволяет снизить количество операций умножения и вычитания, а следовательно, сократить время и ресурсы, затрачиваемые на деление многочленов. Схема Горнера основывается на идее факторизации многочлена и введении новых переменных, что позволяет минимизировать число необходимых операций.
Благодаря использованию схемы Горнера, можно добиться более быстрого и эффективного выполнения деления многочленов, что является важным фактором при решении различных задач. Кроме того, схема Горнера позволяет упростить математические вычисления и уменьшить вероятность возникновения ошибок.
В итоге, преимущества схемы Горнера по сравнению с классическим делением заключаются в сокращении числа операций умножения и вычитания, снижении временных затрат и улучшении эффективности вычислений.



