Физика - это наука, исследующая законы природы и ее явления. Одной из основных задач физики является измерение различных физических величин, в том числе и длины. Длина - это фундаментальная величина, которая определяет размеры объектов и является одним из главных параметров при описании окружности.
Окружность, в свою очередь, является геометрической фигурой, состоящей из всех точек плоскости, равноудаленных от одной фиксированной точки, называемой центром. Когда речь идет о измерении длины окружности, важную роль играет математическая формула, связывающая длину окружности с ее радиусом или диаметром.
Формула длины окружности была впервые выведена античными математиками и философами. Согласно этой формуле, длина окружности равна произведению числа Пи на удвоенный радиус или на диаметр окружности. То есть, L = 2πR или L = πd, где L - длина окружности, π (пи) - число, приближенно равное 3,14159, R - радиус, d - диаметр окружности.
Законы физики и математические формулы позволяют измерить длину окружности, что является важным для многих научных и технических областей. Измерение длины окружности имеет широкое применение в инженерии, архитектуре, физике, астрономии и других науках. Правильное определение и измерение длины окружности позволяют решать задачи проектирования, моделирования и строительства объектов, а также проводить точные научные исследования.
Физика: законы и измерение длины окружности
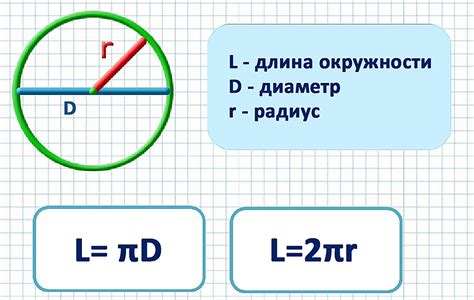
Один из основных законов, связанных с измерением длины окружности, это закон Архимеда. Он утверждает, что длина окружности равна произведению ее диаметра на число π (пи). Другими словами, если диаметр окружности равен D, то ее длина равна L = πD.
Также, в контексте измерения длины окружности, важно упомянуть закон Галилея. Он сформулировал связь между окружностью и другими геометрическими фигурами. Главное, что закон Галилея нам говорит, что окружность является самой короткой линией, соединяющей две точки на плоскости. То есть, если нам нужно пройти из одной точки в другую, самым быстрым путем будет идти по окружности. Именно поэтому окружности так широко используются в архитектуре, инженерии и других областях.
Измерение длины окружности играет важную роль в различных научных и практических областях. Например, в строительстве и инженерии часто возникает необходимость определить длину круговых объектов, таких как кабели, трубы или дорожные знаки. Математики и физики используют измерение длины окружности при решении дифференциальных уравнений и изучении формы геометрических фигур.
Итак, физика играет важную роль в изучении и измерении длины окружности, устанавливая законы и связи между этим геометрическим параметром и другими физическими явлениями. Знание этих законов и применение физических принципов позволяют нам более точно измерять и использовать окружности в различных научных и практических областях.
Законы: фундаментальные принципы физики

Существует несколько фундаментальных законов физики, которые являются основой для понимания многообразных явлений и процессов. Они описывают взаимодействия между частицами и объектами, а также устанавливают принципы сохранения различных величин.
Один из основополагающих законов физики - закон сохранения энергии. Согласно этому закону, энергия не может быть создана или уничтожена, она может только передаваться и преобразовываться из одной формы в другую. Также существует закон сохранения импульса, гласящий, что сумма импульсов системы частиц остается неизменной, если на систему не действуют внешние силы.
Другим важным фундаментальным принципом физики является закон всемирного тяготения. Этот закон, открытый Исааком Ньютоном, описывает гравитационное взаимодействие между объектами. Согласно этому закону, каждый объект притягивает другой объект с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
| Закон | Физический принцип |
|---|---|
| Закон Архимеда | Тело, погруженное в жидкость, испытывает всплывающую силу, равную весу вытесненной жидкости. |
| Закон Ома | Сила тока, проходящего через проводник, прямо пропорциональна напряжению и обратно пропорциональна сопротивлению данного проводника. |
| Закон Гука | Деформация упругого тела прямо пропорциональна приложенной силе. |
Эти и другие фундаментальные законы физики помогают ученым понять и объяснить множество явлений в природе. Они лежат в основе многих научных и технологических достижений, а также применяются в различных областях жизни, от разработки новых материалов до построения ракет.
Длина окружности: определение и свойства
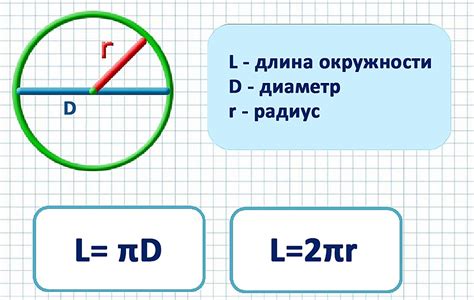
C = 2πr
где C - длина окружности, π - математическая константа, приблизительно равная 3,14159, а r - радиус окружности.
Стоит отметить, что длина окружности является пропорциональной ее радиусу. То есть увеличение радиуса на определенное значение приведет к пропорциональному увеличению длины окружности. Также стоит отметить, что все окружности с одинаковым радиусом имеют одинаковую длину.
Свойство окружности заключается в том, что ее длина является кратной длины диаметра, который является прямой линией, соединяющей две точки окружности, проходящие через ее центр. Соотношение между длиной окружности и диаметром описывается формулой:
C = πd
где С - длина окружности, π - математическая константа, приблизительно равная 3,14159, а d - диаметр окружности.
Из этих формул следует, что длина окружности является ключевой характеристикой этой геометрической фигуры и позволяет определить ее размер. Знание длины окружности позволяет решать различные задачи, связанные с этой фигурой, в том числе в физике, геометрии и инженерии.
Закон сохранения энергии: влияние на измерение

Влияние закона сохранения энергии на измерение длины окружности состоит в том, что энергия, затрачиваемая на измерение длины окружности, также должна сохраняться.
При измерении длины окружности используется специальное устройство - ленточная мера. Когда лента обжимается вокруг окружности, на нее действует сила натяжения, которая затрачивает некоторую энергию. Согласно закону сохранения энергии, эта энергия должна быть равной энергии, получаемой при растягивании ленты обратно в исходное положение.
Таким образом, при измерении длины окружности необходимо учесть энергию, затрачиваемую на натяжение ленты. Если это не будет учтено, измерения могут быть неточными.
Учет энергии при измерении длины окружности позволяет получить более точные результаты и обеспечить соблюдение закона сохранения энергии в процессе измерения.
Формулы: математические выражения и расчеты

Для изучения длины окружности и применения законов физики, необходимо знать некоторые основные формулы и математические выражения, которые помогут провести необходимые расчеты.
Одной из основных формул, связывающих длину окружности с ее радиусом, является формула длины окружности:
C = 2πr
где C - длина окружности, а r - радиус окружности.
Эта формула позволяет быстро и просто вычислить длину окружности, зная ее радиус.
Также, при изучении законов физики и проведении экспериментов часто используется формула для расчета площади окружности:
S = πr²
где S - площадь окружности, а r - радиус окружности.
Эта формула позволяет определить площадь поверхности окружности и использовать ее в дальнейших расчетах.
Изучение законов физики и проведение экспериментов требует также умения считать и проводить математические операции. Например, для расчета длины окружности или площади окружности можно использовать следующие действия:
- Вычисление радиуса окружности по формуле r = D/2, где D - диаметр окружности.
- Подстановка значения радиуса в формулы для расчета длины окружности (C = 2πr) и площади окружности (S = πr²).
- Умножение и деление, используя значение числа π (пи), которое обычно принимается равным 3,14 или 3,1415.
Используя эти формулы и математические операции, можно проводить точные расчеты и получать достоверные результаты, необходимые для изучения законов физики и определения длины окружности.
Инструменты: средства измерения длины окружности

- Лента - один из самых распространенных инструментов для измерения длины. Лента имеет метки и цифры, которые помогают определить длину окружности.
- Шнур - еще один инструмент, который часто используется для измерения длины окружности. Шнур наматывается на окружность и затем прямолинейно разматывается, позволяя получить приближенное значение длины.
- Компас - инструмент, основанный на принципе радиуса окружности. Компас используется для определения радиуса окружности, а затем длина окружности вычисляется по формуле 2πr.
- Лазерный измеритель - современный инструмент, который использует лазерное излучение для измерения расстояний. С его помощью можно точно измерить длину окружности с минимальной погрешностью.
Выбор конкретного инструмента зависит от требуемой точности измерения и условий, в которых проводится измерение. Правильный выбор инструмента позволяет получить точные данные, которые могут быть использованы в дальнейших расчетах и конструкциях.
Связь законов физики и измерения длины окружности
Одним из базовых законов физики, который тесно связан с измерением длины окружности, является закон сохранения энергии. Согласно этому закону, энергия в системе остается постоянной, пусть и может претерпевать преобразования из одной формы в другую. Концепция энергии особенно важна при рассмотрении движения объектов по окружности. Так, например, при движении тела по окружности возникает кинетическая энергия, которая зависит от массы тела и его скорости.
Еще одним законом физики, влияющим на измерение длины окружности, является закон всемирного притяжения, сформулированный Исааком Ньютоном. Этот закон объясняет гравитационное притяжение между телами и позволяет вычислить гравитационную константу, которая, в свою очередь, может быть использована для измерения длины окружности.
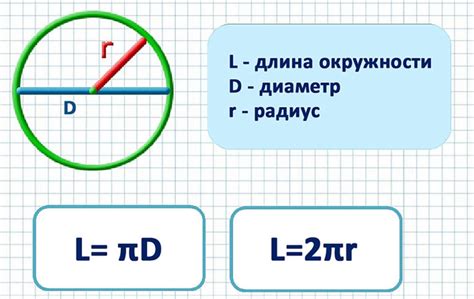
Точное измерение длины окружности также требует применения математических законов и формул. Например, для расчета длины окружности с использованием радиуса или диаметра применяется формула C = πd, где С - длина окружности, π - математическая константа, известная как число «пи», и d - диаметр окружности.
Таким образом, измерение длины окружности является важной задачей физики и требует учета различных законов и формул. Связь между законами физики и измерением длины окружности позволяет улучшить точность и надежность таких измерений, а также исследовать различные аспекты движения и энергии в физических системах.
Практическое применение: примеры из реальной жизни

Законы физики и измерение длины окружности находят широкое применение в различных сферах нашей жизни. Ниже представлены несколько примеров, демонстрирующих практическое использование этих концепций.
| Пример | Область применения |
|---|---|
| Изготовление колес для автомобилей | Автомобильная промышленность |
| Проектирование и строительство круглых стадионов | Архитектура и инженерия |
| Разработка лентопротяжных конвейеров | Производство и логистика |
| Оценка длины резинообразующих полиномов | Химическая промышленность |
| Расчет длины трубопроводов для транспортировки нефти и газа | Нефтегазовая промышленность |
Это лишь некоторые примеры использования законов физики и измерения длины окружности в реальной жизни. Эти концепции играют важную роль в различных областях, способствуя развитию технологий и повышению эффективности процессов. Они помогают нам понимать и прогнозировать поведение физических объектов и создавать более инновационные решения.
Инновации: новые методы измерения длины окружности

Один из инновационных методов измерения длины окружности основан на использовании лазерной технологии. Специальное устройство, оснащенное лазером, проецирует лазерный луч на поверхность окружности. Затем с помощью специального датчика измеряется угловое положение точки пересечения лазерного луча и окружности. Зная угловое значение и радиус окружности, можно определить длину окружности с высокой точностью.
Еще один новый метод измерения длины окружности основан на использовании компьютерного зрения. Специальная камера с высоким разрешением фиксирует изображение окружности на плоскости. После этого с помощью программного обеспечения происходит анализ изображения и вычисление длины окружности по формулам геометрии. Этот метод позволяет достичь высокой точности и устранить ошибки, связанные с пользовательским вмешательством.
Еще одним интересным способом измерения длины окружности является использование новых материалов с особыми свойствами. Некоторые материалы приобретают эффект "памяти формы", то есть они могут запомнить свою форму и возвращаться в нее после деформации. Если укрепить специальную полоску такого материала по окружности, а затем выпрямить ее, длина окружности можно будет измерить, просто сравнивая длину полоски до и после деформации.
Таким образом, с развитием науки и технологий появляются новые интересные методы измерения длины окружности. Они позволяют получать более точные результаты и применяться в различных областях науки, техники и производства.



