Закон градиента Гаскелла - это физический закон, описывающий процесс переноса газов через деформируемую пористую среду. Он имеет ключевое значение в геофизике, позволяя вести исследования и прогнозирование различных процессов, связанных с проникновением газов через горные породы. Принцип работы закона градиента Гаскелла основан на взаимосвязи давления и плотности газа, а также на изменении величины и градиента давления.
Основная идея закона градиента Гаскелла заключается в том, что перенос газа осуществляется в результате разности давлений между двумя точками внутри пористой среды. Если разница давлений между точками равна нулю, то градиент давления также равен нулю, и в этом случае перенос газа не происходит. Следовательно, для переноса газа необходимо создать разность давлений внутри среды. Это можно сделать путем изменения давления в одной из точек или изменения величины пористости.
Согласно закону градиента Гаскелла, процесс переноса газа является неравномерным и зависит от градиента давления и проницаемости пористой среды. Чем больше градиент давления между точками, тем интенсивнее будет происходить перенос газа. Важной особенностью закона градиента Гаскелла является то, что при одинаковых значениях градиента давления в разных средах, скорость переноса газа будет различаться в зависимости от их проницаемости.
Закон градиента Гаскелла и его работа
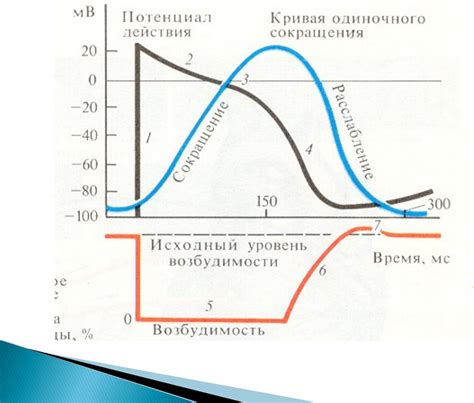
Работа закона градиента Гаскелла состоит из нескольких этапов:
- Рассчитывается производная функции активации нейронной сети.
- Рассчитывается градиент, который представляет собой сумму производных функций активации всех нейронов в сети.
- Рассчитывается изменение весов нейронов, которое пропорционально градиенту.
- Изменение весов применяется к нейронам, и процесс повторяется до достижения определенного условия остановки, такого как достижение минимума ошибки или определенного количества итераций.
Основная идея закона градиента Гаскелла заключается в том, что частные производные показывают, какое изменение весов приведет к улучшению или ухудшению общей ошибки нейронной сети. Путем изменения весов сети в направлении, противоположном градиенту, можно достичь более точного предсказания и уменьшить ошибку обучения.
Однако, при работе с градиентом Гаскелла необходимо обращать внимание на несколько особенностей:
- Подбор правильного коэффициента обучения - слишком большое значение может привести к неустойчивости обучения, а слишком маленькое значение - к медленной сходимости.
- Решение проблемы затухающего или взорвавшегося градиента - большие градиенты могут вызывать неустойчивость или расходимость сети, поэтому иногда производятся изменения в алгоритмах оптимизации градиента.
- Подбор начальных значений весов - исходные значения весов могут влиять на сходимость сети, поэтому для улучшения обучения часто используется случайная инициализация весов.
Закон градиента Гаскелла является основой для большинства алгоритмов обучения нейронных сетей и играет важную роль в достижении хорошей производительности сети.
Принцип работы закона градиента Гаскелла
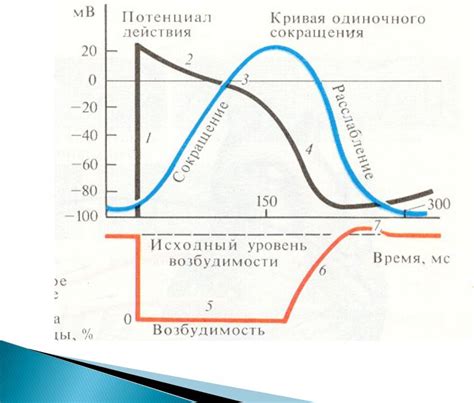
Принцип работы закона градиента Гаскелла обусловлен действием двух факторов: концентрационного и температурного градиентов. Концентрационный градиент возникает в результате различия концентраций вещества в разных частях раствора. Температурный градиент образуется, когда температура раствора неоднородна.
Взаимодействие концентрационного и температурного градиентов приводит к передвижению частиц вещества из области высокой концентрации и температуры в область низкой концентрации и температуры. Этот процесс называется диффузией и является результатом случайного движения молекул вещества.
Для более точного описания процесса диффузии, закон градиента Гаскелла использует математическое выражение, которое связывает поток диффузии с концентрационным и температурным градиентами. Формула закона градиента Гаскелла имеет вид:
| Диффузионный поток | = | Коэффициент диффузии | × | Площадь поперечного сечения | × | Концентрационный градиент | × | Температурный градиент |
|---|
Эта формула позволяет рассчитать объем вещества, переносящегося при диффузии через площадку поперечного сечения за единицу времени.
Закон градиента Гаскелла имеет множество практических применений. Например, он используется в процессах очистки воды и воздуха, в производстве лекарственных препаратов, в химической и биологической аналитике. Понимание принципа работы закона градиента Гаскелла позволяет улучшить эффективность и качество этих процессов.
Особенности закона градиента Гаскелла
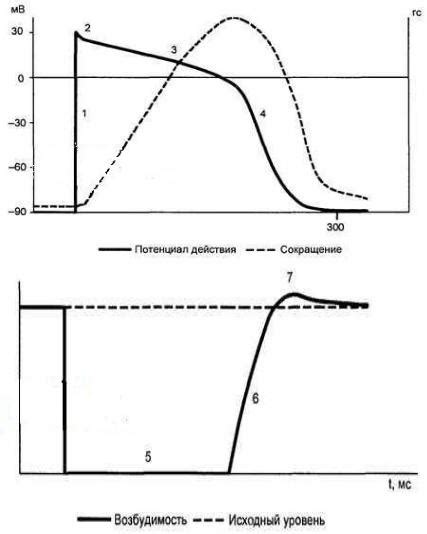
Основные особенности закона градиента Гаскелла:
| 1. | Итеративность | – алгоритм выполняет серию итераций, на каждой которой параметры модели обновляются в соответствии с градиентом функции потерь. |
| 2. | Градиентный спуск | – алгоритм использует метод градиентного спуска, который позволяет найти локальный минимум функции потерь в многомерном пространстве параметров модели. |
| 3. | Градиент | – алгоритм вычисляет градиент функции потерь по параметрам модели. Градиент представляет собой вектор, указывающий направление наиболее быстрого убывания функции потерь. |
| 4. | Шаг обновления | – алгоритм использует параметр шага обновления (learning rate), которое определяет размер шага при обновлении параметров модели. Неправильно выбранный шаг может привести к медленной сходимости или расхождению алгоритма. |
| 5. | Минимизация функции потерь | – основная цель алгоритма заключается в минимизации функции потерь, что позволяет получить оптимальные параметры модели для предсказания целевой переменной. |
| 6. | Применимость к линейным и нелинейным моделям | – закон градиента Гаскелла может быть применен как к линейным моделям, так и к нелинейным моделям машинного обучения. |
Все эти особенности делают закон градиента Гаскелла мощным инструментом для обучения моделей машинного обучения и повышения их точности и эффективности.



