Ромб - это четырехугольник, у которого все стороны равны между собой. Этот геометрический объект обладает множеством интересных свойств, включая свою уникальную высоту, которая также является важным атрибутом ромба.
Высота ромба - это перпендикуляр, опущенный из одной вершины ромба к противоположной стороне. Она соединяет середины двух противоположных сторон и делит ромб на два равных треугольника. Эти треугольники могут быть использованы для вычисления площади ромба.
Важно отметить, что высота ромба всегда перпендикулярна соответствующей стороне и делит ее на две равные отрезки. Более того, высота ромба является осью симметрии для фигуры, что означает, что зеркальное отражение относительно этой линии приведет к полной идентичности ромба.
Примеры использования высоты ромба можно найти во многих сферах нашей жизни. Например, в строительстве она может быть использована для определения площади крыши или фасада ромбовидной формы. В геометрии высота ромба может использоваться для нахождения его площади или для определения расстояния между параллельными сторонами ромба.
Определение высоты ромба
Высота ромба является основным свойством этой фигуры, которое отображает насколько высоким или низким является данный ромб. Так как ромб является параллелограммом, все его стороны равны между собой, и высота является перпендикуляром к этим сторонам.
Высота ромба играет важную роль в решении различных задач, связанных с этой фигурой. Она может быть использована для вычисления площади ромба или для определения других свойств и параметров ромба, например, диагоналей, углов или длины сторон.
Как и в случае с другими геометрическими фигурами, высота ромба можно вычислить с использованием геометрических формул, а также с помощью теорем и свойств, характерных для ромбов.
Примером ромба с высотой может служить изображение шахматной доски, где каждая клетка шахматной доски представляет собой ромб с одинаковыми сторонами и высотой.
Свойства высоты ромба
Свойства высоты ромба:
- Равенство диагоналей: Высота ромба делит его диагонали пополам. То есть, отрезок высоты равен половине длины каждой диагонали.
- Перпендикулярность: Высота ромба перпендикулярна к каждой из его сторон. Это означает, что угол между высотой и стороной равен 90 градусам.
- Кратчайшая дистанция: Высота ромба является кратчайшим расстоянием между параллельными сторонами ромба. Это свойство может быть использовано для нахождения площади ромба через длину одной его высоты.
- Соотношение с другими сторонами: Для ромба с длиной стороны а и высотой h, справедливо следующее соотношение: h = a * sin(α), где α - угол, образованный стороной ромба и его высотой. Это соотношение можно использовать для нахождения высоты ромба по длине его стороны.
Используя эти свойства, можно упростить задачи по нахождению различных параметров ромба и использовать высоту для решения геометрических проблем.
Примеры высоты ромба
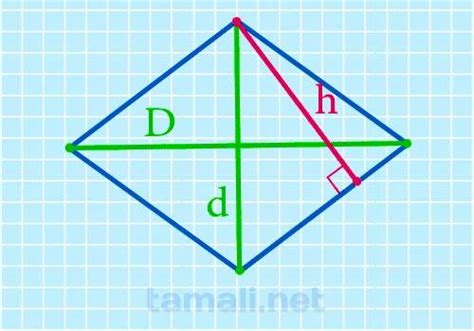
Рассмотрим несколько примеров, чтобы более понятно было представление о высоте ромба:
| Пример | Сторона ромба | Высота ромба |
|---|---|---|
| Пример 1 | 4 см | 3.08 см |
| Пример 2 | 6 см | 4.62 см |
| Пример 3 | 9 см | 6.92 см |
| Пример 4 | 12 см | 9.23 см |
Как можно видеть из примеров, высота ромба не является простым числом и зависит от длины его стороны. Чтобы найти высоту ромба, можно использовать соответствующую формулу или провести геометрическую конструкцию, соединив вершины ромба с центром и построив высоту.
Как найти высоту ромба

- Используя формулу для высоты ромба:
- Измерив диагонали:
- С использованием треугольников:
h = 2 * A / B
где h - высота ромба, A - площадь ромба, B - длина основания ромба.
1) Найдите длину одной из диагоналей ромба. Для этого можно использовать теорему Пифагора:
d₁ = √(a² + b²)/2
где d₁ - длина диагонали, a и b - длины сторон ромба.
2) Найдите высоту ромба, используя найденную длину диагонали и формулу:
h = 2 * A / d₁
где h - высота ромба, A - площадь ромба, d₁ - длина одной из диагоналей.
1) Разделите ромб на два равнобедренных треугольника путем проведения высоты.
2) Найдите высоту одного из треугольников, используя формулу:
h₁ = (2 * A₁) / a₁
где h₁ - высота одного из треугольников, A₁ - площадь одного из треугольников, a₁ - длина основания одного из треугольников.
3) Высота ромба будет равна высоте одного из треугольников.
Какой бы способ вы не выбрали, помните о важности правильного измерения и использования соответствующих формул для расчета высоты ромба.



