Четырехугольник – это геометрическая фигура, состоящая из четырех сторон, которые соединяются четырьмя вершинами. Он является одной из основных фигур в геометрии и широко используется как в научных исследованиях, так и в практических приложениях.
Важно отметить, что существует несколько типов четырехугольников, каждый из которых обладает своими уникальными свойствами. Например, прямоугольник является частным случаем четырехугольника, у которого все углы равны 90 градусов.
Свойства четырехугольников могут быть различными и зависят от типа фигуры. Некоторые из основных свойств четырехугольников включают:
- Сумма внутренних углов: в любом четырехугольнике сумма всех его внутренних углов равна 360 градусов.
- Диагонали: четырехугольник имеет две диагонали, которые соединяют противоположные вершины. Диагонали могут быть разной длины и могут иметь различные взаимное положение.
- Симметрия: некоторые четырехугольники обладают осевой симметрией, что означает, что они могут быть разделены на две симметричные половины относительно оси.
Это лишь некоторые из основных свойств четырехугольников. Изучение и понимание этих свойств играет важную роль в геометрии и математике в целом, а также находит практическое применение в различных областях, таких как архитектура, строительство и дизайн.
Четырехугольник
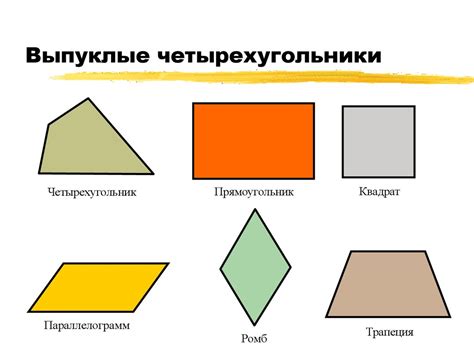
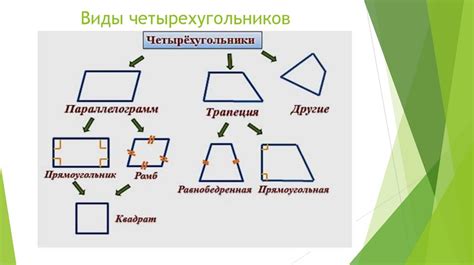
В зависимости от своей структуры и свойств, четырехугольники могут быть классифицированы. Самый общий классификатор основывается на типе углов, образованных сторонами четырехугольника. Вот некоторые основные типы четырехугольников:
| Тип четырехугольника | Описание |
|---|---|
| Прямоугольник | Четырехугольник, у которого все углы являются прямыми углами (90 градусов) |
| Квадрат | Прямоугольник, у которого все стороны равны друг другу |
| Параллелограмм | Четырехугольник, у которого противоположные стороны параллельны друг другу |
| Ромб | Параллелограмм, у которого все стороны равны друг другу |
| Трапеция | Четырехугольник, у которого две противоположные стороны параллельны друг другу |
Каждый тип четырехугольника имеет свои уникальные свойства и формулы для вычисления площади и периметра. Они также могут быть использованы в различных контекстах, таких как архитектура, инженерия и графика.
Изучение четырехугольников имеет большое значение, поскольку они являются основой для более сложных фигур и имеют множество применений в реальном мире.
Определение и классификация
Четырехугольники могут классифицироваться по различным признакам:
- По виду сторон: равнобедренные, прямоугольные, ромбы, параллелограммы и т. д.
- По виду углов: прямоугольные, остроугольные, тупоугольные и т. д.
- По взаимному расположению сторон и углов: выпуклые, невыпуклые, самопересекающиеся и т. д.
Классификация четырехугольников помогает систематизировать и изучать их свойства и характеристики. Каждый класс четырехугольников имеет свои особенности и свойства, которые делают их уникальными внутри своего класса.
Свойства четырехугольников

1. Углы четырехугольника:
У каждого четырехугольника сумма внутренних углов равна 360 градусов. Это свойство называется сумма углов четырехугольника.
2. Стороны четырехугольника:
Четырехугольник может быть равнобоким, когда его все стороны равны, или неравнобоким, когда хотя бы две стороны отличаются по длине. Также существуют специальные виды четырехугольников, например, квадрат (все стороны и углы равны) или прямоугольник (два противоположных угла равны 90 градусам).
3. Диагонали четырехугольника:
Диагоналями четырехугольника называются отрезки, соединяющие его вершины. У параллелограмма (четырехугольника с противоположными сторонами, параллельными и равными) диагонали равны между собой и делятся пополам. У прямоугольника и ромба диагонали также равны между собой. Диагонали возможны только в выпуклых четырехугольниках.
4. Специальные свойства:
Существуют множество четырехугольников с особыми свойствами, например, трапеция (имеет хотя бы одну пару параллельных сторон) или ромб (все стороны равны, диагонали перпендикулярны). Каждый вид четырехугольника имеет свои уникальные характеристики.
Типы четырехугольников
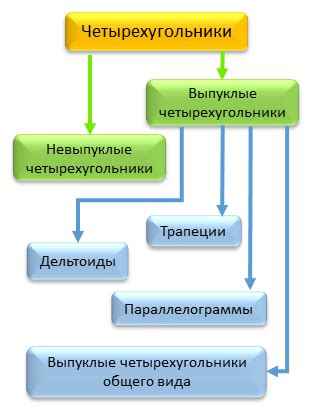
В зависимости от свойств сторон и углов, четырехугольники могут быть классифицированы на различные типы:
- Прямоугольник: четырехугольник, у которого все углы прямые.
- Квадрат: четырехугольник, у которого все стороны равны и все углы прямые.
- Ромб: четырехугольник, у которого все стороны равны.
- Параллелограмм: четырехугольник, у которого противоположные стороны параллельны.
- Трапеция: четырехугольник, у которого хотя бы две стороны параллельны.
- Равнобедренная трапеция: трапеция, у которой боковые стороны равны.
- Необходикивидесятиугольник: четырехугольник, у которого все внутренние углы меньше 90 градусов.
- Тупоугольник: четырехугольник, у которого один из внутренних углов больше 90 градусов.
Каждый из этих типов четырехугольников имеет свои особенности и свойства, которые используются при решении задач геометрии.
Площадь и периметр
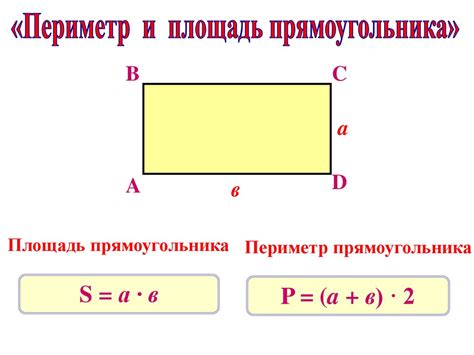
Для прямоугольников площадь вычисляется по формуле: S = a * b, где a и b - длины сторон прямоугольника. Для других типов четырехугольников, площадь можно вычислить с помощью формулы Герона для выпуклых четырехугольников или разделением фигуры на треугольники.
Периметр четырехугольника - это сумма длин всех его сторон. Периметр можно вычислить, просуммировав длины всех сторон четырехугольника.
Зная площадь и периметр четырехугольника, можно извлечь дополнительную информацию о фигуре, например, вычислить значения диагоналей, радиус описанной окружности или вписанной окружности, а также другие характеристики и свойства.
Углы и диагонали

Четырехугольник имеет четыре угла. Сумма всех углов внутри четырехугольника равна 360 градусов.
Диагонали четырехугольника являются отрезками, соединяющими вершины, не являющиеся соседними. Четырехугольник содержит две диагонали.
Углы, образованные диагоналями и сторонами четырехугольника, называются диагональными углами.
Если четырехугольник является выпуклым, то каждая пара диагональных углов смежная и их сумма равна 180 градусов. Если же четырехугольник является невыпуклым, то сумма диагональных углов может быть как меньше, так и больше 180 градусов.
Диагонали также обладают свойством пересекаться внутри четырехугольника, то есть они имеют общую точку пересечения. Точка пересечения диагоналей называется центром четырехугольника.
Зная значения углов и длины диагоналей, можно найти другие характеристики четырехугольника, такие как периметр, площадь или радиус вписанной окружности.
Примеры применения четырехугольников
Четырехугольники находят применение во многих областях науки, техники и ежедневной жизни. Ниже приведены некоторые примеры использования четырехугольников:
- Геометрия: Четырехугольники широко используются в геометрии для изучения и классификации фигур. Они могут быть выпуклыми или невыпуклыми, правильными или неправильными.
- Архитектура: В строительстве четырехугольники применяются для определения формы зданий, окон, дверей и других элементов. Они также используются для расчета площадей и объемов помещений.
- Изготовление мебели: При проектировании и изготовлении мебели, такой как столы, стулья, шкафы и кровати, четырехугольники используются для определения формы и размеров.
- Картография: Четырехугольники применяются для определения границ и формы земельных участков на картах и планах.
- Инженерия: В инженерных расчетах и моделировании четырехугольники используются для определения формы и размеров объектов, а также для определения взаимного расположения элементов конструкции.
- Игры и головоломки: Четырехугольники часто используются в играх и головоломках, таких как танграм, пазлы, судоку и различные геометрические игры.
- Машинное зрение: В компьютерном зрении и распознавании образов четырехугольники используются для определения формы объектов и областей на изображениях.
Это лишь некоторые из множества примеров использования четырехугольников в различных областях. Их универсальность и простота делают их важным инструментом для анализа и моделирования различных форм и конструкций.



