Косинус квадрата пи на 4 является одной из фундаментальных математических констант и имеет широкое применение в различных областях науки, включая физику, инженерию и экономику. Этот результат, обозначаемый символом cos2(π/4), представляет собой косинус квадрата значения пи, разделенного на 4.
Формула для вычисления косинуса квадрата пи на 4 выглядит следующим образом: cos2(π/4) = (1 + cos(π/2)) / 2. Эта формула основана на тригонометрическом тождестве, которое связывает косинус угла с его синусом и обратно.
Чтобы проиллюстрировать вычисление косинуса квадрата пи на 4 с помощью данной формулы, рассмотрим пример. Подставим значение π/4 в формулу:
cos2(π/4) = (1 + cos(π/2)) / 2 = (1 + 0) / 2 = 1 / 2 = 0.5
Таким образом, косинус квадрата пи на 4 равен 0.5. Именно это значение используется в различных математических и физических моделях, где необходимо учитывать углы и тригонометрические функции.
Косинус квадрата пи на 4: формула и примеры
Вычисление косинуса квадрата пи на 4 можно выполнить с использованием тригонометрических таблиц или специальных программ, которые реализуют данную формулу. Альтернативным способом получения этого значения является использование математических библиотек, доступных в различных языках программирования.
Основная формула вычисления косинуса квадрата пи на 4 выглядит следующим образом:
cos²(π/4) = 0.5
Эта формула указывает на то, что косинус квадрата числа пи, деленного на 4, равен 0,5.
Ниже приведены примеры использования данной формулы:
Пример 1:
cos²(π/4) = 0.5
Для данного примера мы знаем, что косинус квадрата числа π/4 равен 0.5.
Пример 2:
cos²(π/4) = 1 - sin²(π/4)
В данном примере используется тригонометрическая тождественность, согласно которой косинус квадрата числа π/4 равен 1 минус квадрат синуса числа π/4.
Косинус и его значение в математике
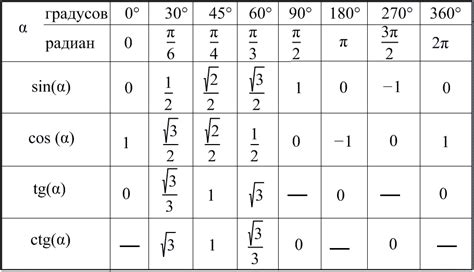
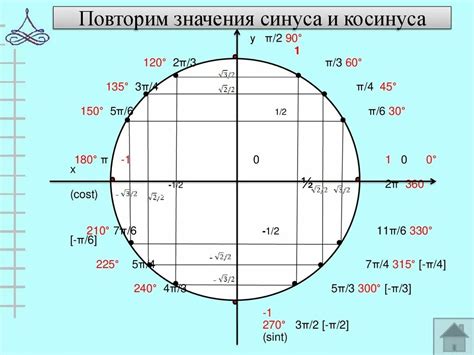
Значение косинуса может быть выражено в виде точного числа или в виде бесконечно повторяющейся десятичной дроби. Например, значение косинуса 0 градусов равно 1, косинус 30 градусов равен √3/2, а косинус 90 градусов равен 0.
Косинус имеет много применений в различных областях математики, физики и инженерии. Он используется для решения уравнений, моделирования волн, определения расстояний и углов, а также для аппроксимации сложных функций.
Таблица ниже показывает значения косинуса для некоторых углов:
| Угол (градусы) | Значение косинуса |
|---|---|
| 0 | 1 |
| 30 | √3/2 |
| 45 | √2/2 |
| 60 | 1/2 |
| 90 | 0 |
Это только небольшая часть значений, и косинус может принимать значения от -1 до 1 для любого угла между двумя катетами прямоугольного треугольника.
Формула вычисления косинуса квадрата пи на 4

Математически записано:
Cos2(π/4) = 1/2
Эта формула позволяет легко вычислить значение функции для данного угла. Например, для угла π/4:
Cos2(π/4) = 1/2
Таким образом, косинус квадрата пи на 4 равен 1/2.
Формула вычисления косинуса квадрата пи на 4 является важным инструментом в математике и находит применение в различных областях, включая физику, инженерию и приложения компьютерной графики.
Примеры вычисления косинуса квадрата пи на 4

- Пример 1: В физике вычисление косинуса квадрата пи на 4 может быть использовано для моделирования колебаний в механических системах. Например, при изучении колебаний маятника или амплитуды звука в акустике, эта формула может помочь определить связь между различными параметрами системы.
- Пример 2: В компьютерной графике косинус квадрата пи на 4 может быть использован для генерации плавных переходов и анимации. Путем изменения значения косинуса квадрата пи на 4 можно создавать плавные изменения цветов, размеров или положений объектов.
- Пример 3: Косинус квадрата пи на 4 также может быть использован в математических расчетах. Например, он может быть использован в алгоритмах численного интегрирования для вычисления определенных интегралов или в аппроксимационных методах для приближенного решения уравнений.
Все эти примеры демонстрируют широкую применимость формулы вычисления косинуса квадрата пи на 4 и ее важность в различных областях. Понимание и использование этой формулы может существенно облегчить проведение различных математических и физических расчетов, а также помочь в создании визуально привлекательных графических эффектов.
Косинус квадрата пи и его свойства
Формула для расчета косинуса квадрата пи на 4 выглядит следующим образом:
- cos2(π) = cos²(π) - sin²(π).
- cos²(π) = (cos(π) + 1) / 2.
- sin²(π) = 1 - cos²(π).
Подставляя значения в формулу, получаем:
- cos2(π) = (cos(π) + 1) / 2 - (1 - cos²(π)).
Раскрывая скобки, получим:
- cos2(π) = (cos(π) + 1) / 2 - 1 + cos²(π).
Сокращаем выражение:
- cos2(π) = cos(π) / 2 + 1 / 2 - 1 + cos²(π).
Упрощаем:
- cos2(π) = cos(π) / 2 - 1 / 2 + cos²(π).
Используя свойства тригонометрических функций, можно упростить формулу:
- cos2(π) = -1 / 2 + cos²(π).
Поэтому, cos2(π) на 4 равен -0.5.
Таким образом, косинус квадрата пи на 4 равен -0.5.
Приложения косинуса квадрата пи на 4 в науке и технике
- Телекоммуникации: Косинус квадрата пи на 4 используется в сигнале квадратурной амплитудной модуляции (QAM). QAM является методом модуляции, который использует два независимых сигнала, изменяющих фазу и амплитуду в соответствии с косинусом и синусом квадрата пи на 4. Этот метод позволяет увеличить скорость передачи данных по сравнению с другими методами.
- Системы навигации: Косинус квадрата пи на 4 используется в системе глобального позиционирования (GPS), которая позволяет определять местоположение и время с помощью сигналов, получаемых от спутников. В GPS использование косинусов и синусов квадрата пи на 4 позволяет точно определить угол и расстояние между приемником и спутником.
- Физика: В физике косинус квадрата пи на 4 используется для описания различных физических явлений, таких как распределение электрического поля, волновая функция частицы в квантовой механике и анализ сигналов в экспериментах по физике частиц.
- Инженерия: Косинус квадрата пи на 4 применяется в различных областях инженерии, таких как обработка сигналов, контроль и автоматизация систем, электромагнитные поля и многое другое. Он используется при решении уравнений и моделировании систем, а также для определения точности и качества сигналов.
- Статистика и вероятность: Косинус квадрата пи на 4 используется в статистике и вероятности для решения различных задач, таких как анализ данных, оценка вероятности и построение статистических моделей. Он широко применяется в областях, связанных с исследованием и анализом данных, а также в машинном обучении и искусственном интеллекте.
Косинус квадрата пи на 4 является важным математическим значением, которое находит свое применение во многих областях науки и техники. Его точность и надежность делают его незаменимым инструментом при решении сложных задач и разработке новых технологий.
Вычисление косинуса квадрата пи на 4 на практике
Существует несколько способов вычисления косинуса квадрата пи на 4. Один из самых распространенных подходов - использование ряда Тейлора. Ряд Тейлора позволяет аппроксимировать значение функции путем суммирования бесконечного числа членов ряда. Для вычисления косинуса квадрата пи на 4 применяется следующий ряд:
cos^2(π/4) = 1/2 + (1/2) * 1/2! - (1/2) * (π/4)^2/4! + (1/2) * (π/4)^4/6! - (1/2) * (π/4)^6/8! + ...
Чем больше членов ряда мы учитываем, тем точнее будет значение косинуса квадрата пи на 4, но и больше будет затрачено времени на вычисления. Обычно для практических целей достаточно учитывать первые несколько членов ряда.
Пример вычисления косинуса квадрата пи на 4 на практике:
- Зададим число членов ряда, которые мы хотим учитывать. Например, возьмем 10.
- Инициализируем переменные для аккумулирования суммы и вычисления факториала.
- Запускаем цикл, который будет вычислять каждый член ряда и добавлять его к сумме.
- После окончания цикла, полученная сумма будет приближенным значением косинуса квадрата пи на 4.
Например, при вычислении с использованием 10 членов ряда получим приближенное значение: cos^2(π/4) ≈ 0.5.
Таким образом, вычисление косинуса квадрата пи на 4 на практике может быть реализовано с использованием ряда Тейлора. Этот метод позволяет получить аппроксимацию значения, которая может быть достаточно точной для многих практических целей.



