Внетабличное умножение и деление – это методы вычислений, которые позволяют производить умножение и деление чисел без использования таблицы умножения или деления, а лишь с помощью умения работать с числами и основных арифметических операций.
Основной принцип внетабличного умножения и деления заключается в том, чтобы разложить число на составные части, которые можно проще перемножить или поделить. Например, вместо того, чтобы умножать двузначные числа в столбик, можно разложить каждое число на десятки и единицы, а затем перемножить эти составные части отдельно.
Пример умножения:
Умножим число 27 на число 36. Разложим каждое число на десятки и единицы:
27 = 20 + 7
36 = 30 + 6
Теперь перемножим составные части чисел:
(20 + 7) * (30 + 6) = 20 * 30 + 7 * 30 + 20 * 6 + 7 * 6 = 600 + 210 + 120 + 42 = 972
Таким образом, результатом умножения чисел 27 и 36 без использования таблицы умножения получаем число 972.
Внетабличное умножение: суть и методы расчета

Основным методом внетабличного умножения является метод разложения на множители. Этот метод состоит в разложении каждого из чисел на простые множители и последующем перемножении этих множителей. Например, если нужно найти произведение чисел 24 и 36, то мы можем разложить каждое из них на множители:
| Число | Множители |
|---|---|
| 24 | 2 × 2 × 2 × 3 |
| 36 | 2 × 2 × 3 × 3 |
Затем перемножив все множители, мы получим искомое произведение:
24 × 36 = (2 × 2 × 2 × 3) × (2 × 2 × 3 × 3) = 2 × 2 × 2 × 2 × 3 × 3 × 3 = 2592
Таким образом, произведение чисел 24 и 36 равно 2592.
Кроме метода разложения на множители, существуют и другие методы внетабличного умножения, такие как метод двоичного внетабличного умножения, метод множителей и другие. Каждый из них имеет свои особенности и может быть применен в различных случаях для упрощения расчетов.
Понятие и основные принципы
Основные принципы внетабличного умножения и деления включают:
- Использование известных фактов о числах и арифметических операциях для упрощения задач;
- Разбиение сложных задач на более простые подзадачи;
- Использование метода приближения для быстрого нахождения ответов;
- Выполнение вычислений в определенном порядке для минимизации ошибок.
Внетабличное умножение и деление являются важными навыками для развития математического мышления, улучшения скорости вычислений и повышения точности результатов.
Умножение чисел с разрядностью более 9

Умножение чисел с разрядностью более 9 осуществляется по тому же принципу, что и умножение чисел с разрядностью до 9. Основное отличие заключается лишь в увеличении количества разрядов и расширении алгоритма умножения.
При умножении чисел с разрядностью более 9 представление числа может быть записано в виде последовательности разрядов, где каждый разряд представляет определенную степень числа 10. Например, число 123456789 будет представлено в виде разрядов: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Для умножения чисел с разрядностью более 9 необходимо выполнить следующие шаги:
- Разделить каждое число на разряды и записать их в виде последовательности разрядов.
- Выполнить умножение каждого разряда первого числа на каждый разряд второго числа с учетом позиции разряда.
- Сложить полученные произведения разрядов, учитывая их позицию.
- Сократить полученную сумму до одного числа, представленного в виде разрядов.
Пример умножения чисел с разрядностью более 9:
12345 × 6789 ------ 74005 74040 7405 61710 12345 ------ 83668205
В результате умножения числа 12345 на число 6789 получается число 83668205.
Алгоритм умножения больших чисел

Умножение больших чисел может быть достаточно сложной задачей, особенно когда числа имеют много разрядов. Однако, существует эффективный алгоритм, который позволяет умножать такие числа без особых проблем.
Одним из наиболее распространенных алгоритмов умножения больших чисел является алгоритм "столбиком". В основе этого алгоритма лежит принцип поэтапного перемножения разрядов чисел, начиная с младших.
Для начала, два числа записываются одно под другим в столбик. Затем, начиная с самого правого разряда, каждая цифра первого числа умножается на каждую цифру второго числа. Результаты умножения записываются в столбик под числами, начиная с позиции, соответствующей разряду, на котором производится умножение.
На следующем шаге все полученные результаты сложаются, при этом учитывается разрядность каждого результата. Результаты сложения также записываются в столбик, начиная с позиции, соответствующей разрядам суммы.
В конечном итоге, получается число, состоящее из разрядов суммы всех умножений. Это и есть результат умножения двух больших чисел.
Однако, чтобы выполнить это умножение вручную, потребуется некоторое время и внимание. В современных вычислительных устройствах, такие операции выполняются гораздо быстрее, благодаря использованию аппаратных средств и алгоритмическим оптимизациям.
Таким образом, алгоритм умножения больших чисел позволяет эффективно выполнять умножение чисел с большим количеством разрядов. Он является основой для реализации умножения в различных программах и вычислительных системах.
Метод множителей и его применение

Применение метода множителей обычно связано с работой с большими числами или числами с десятичной точкой. Он основан на том, что каждое число можно представить в виде произведения множителей. При умножении или делении таких чисел можно переставить множители местами для удобства вычислений.
Рассмотрим пример умножения: 3.5 * 4.2.
- Первое число (3.5) можно разделить на множители 3 и 0.5:
- 3.5 = 3 * 0.5
- 4.2 = 4 * 0.2
- 3 * 4 = 12
- 0.5 * 0.2 = 0.1
- 12 + 0.1 = 12.1
Таким образом, результат умножения 3.5 * 4.2 равен 12.1.
Метод множителей позволяет упростить вычисления и сократить количество операций при работе с большими числами. Он также может быть использован для деления и других операций, где необходимо упростить выражение и получить более точный результат.
Внетабличное деление: общая схема и примеры
Общая схема внетабличного деления заключается в следующем:
- Найдите наибольшее число, на которое делитель может быть умножен, чтобы получить число, которое меньше делимого.
- В вычете запишите это число, а результатом деления будет количество раз, сколько вы его умножили.
- Вычтите произведение из делимого.
- Повторяйте шаги 1-3 до тех пор, пока вычитание не даст нулевой остаток. Полученные результаты сложите, чтобы получить частное.
Рассмотрим пример внетабличного деления:
| Dелимое | Делитель | Частное | Остаток |
| 47 | 3 | 0 | 47 |
| 17 | 3 | 5 | 2 |
| 2 | 3 | 15 | -1 (остаток меньше делителя) |
Таким образом, результатом деления 47 на 3 будет 15 с остатком -1.
Чего стоит ожидать от внетабличного деления

Одним из главных преимуществ внетабличного деления является возможность получения более точных результатов. Традиционные таблицы умножения и деления имеют ограниченный набор значений, и для чисел, не входящих в этот набор, приходится использовать приближенные значения. Внетабличное деление позволяет учесть все цифры числа и получить более точный ответ, особенно при работе с десятичными дробями или очень большими числами.
Еще одним преимуществом внетабличного деления является его гибкость. Традиционные таблицы умножения и деления ориентированы на определенный набор чисел и операций. Внетабличное деление позволяет выполнять умножение и деление с любыми числами, включая нецелые числа и отрицательные числа.
Однако, следует помнить, что внетабличное деление требует большего времени и усилий для выполнения, по сравнению с традиционными методами. Внетабличное деление требует использования специальных алгоритмов и вычислительных методов, которые могут быть сложными для понимания или выполнения. Поэтому внетабличное деление может не подходить для быстрых и простых вычислений.
Внетабличное деление – это полезный инструмент для расширения границ и возможностей математических вычислений. Он позволяет получать более точные результаты и работать с различными типами чисел. Однако, его использование требует дополнительных усилий и времени, поэтому его применение следует тщательно обдумывать в зависимости от ситуации.
Связь между умножением и делением чисел

В математике существует ряд правил и свойств, которые определяют связь между умножением и делением чисел:
| Свойство | Умножение | Деление |
|---|---|---|
| Ассоциативность | (а * b) * c = а * (b * c) | (а * b) / c = а * (b / c) |
| Коммутативность | а * b = b * a | - |
| Дистрибутивность | а * (b + c) = а * b + а * c | а / (b + c) ≠ а / b + а / c |
| Обратная операция | - | а / b = а * (1 / b) |
Эти свойства являются основными и позволяют использовать умножение и деление в различных математических операциях, таких как решение уравнений, построение графиков и многих других.
Знание и понимание связи между умножением и делением поможет вам более глубоко изучить математику и применять ее в реальной жизни.
Примеры внетабличного деления
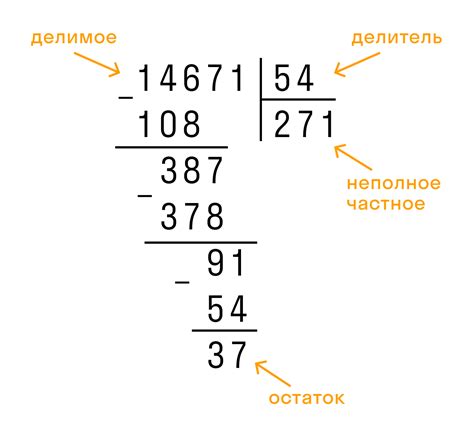
Пример 1:
Деление числа 48 на 6:
1. Выбираем наибольшее число, меньшее 48, и делим на него: 6.
2. Умножаем это число на 10: 6 * 10 = 60.
3. Вычитаем результат из 48: 48 - 60 = -12.
4. Добавляем наибольшее число, меньшее -12, и делим на него: -2.
5. Умножаем это число на 10: -2 * 10 = -20.
6. Вычитаем результат из -12: -12 - (-20) = 8.
7. Ответ: 48 / 6 = 8.
Пример 2:
Деление числа 84 на 7:
1. Выбираем наибольшее число, меньшее 84, и делим на него: 8.
2. Умножаем это число на 10: 8 * 10 = 80.
3. Вычитаем результат из 84: 84 - 80 = 4.
4. Добавляем наибольшее число, меньшее 4, и делим на него: 0.
5. Умножаем это число на 10: 0 * 10 = 0.
6. Вычитаем результат из 4: 4 - 0 = 4.
7. Ответ: 84 / 7 = 12.
Таким образом, внетабличное деление позволяет найти результат деления двух чисел, не прибегая к использованию таблицы умножения.
Полезные советы при проведении внетабличного деления

1. Округление результата: В случае внетабличного деления, часто возникают десятичные числа. Важно помнить, что округление результата должно быть согласовано с задачей и исходными данными. Например, если вы работаете с денежными суммами, может понадобиться округление до определенного количества знаков после запятой.
2. Учет остатка: Внетабличное деление оставляет остаток, который может быть также важной информацией. Остаток от деления может указывать на некоторую закономерность или давать дополнительную информацию о числах, с которыми вы работаете.
3. Будьте внимательны к знакам: Знаки чисел также играют важную роль при внетабличном делении. Не забывайте учитывать положительные и отрицательные значения при проведении деления и записи результата.
4. Проверка результата: После окончания внетабличного деления всегда полезно проверить результат, чтобы убедиться в его правильности. Вы можете сделать это путем обратного умножения или сравнения с другими известными значениями.
5. Применение алгоритмов: Внетабличное деление можно выполнять с помощью различных алгоритмов, включая метод последовательного вычитания, метод неполного частного и другие. Используйте подходящий алгоритм, исходя из поставленной задачи и значения чисел.
Следуя этим полезным советам, вы сможете провести внетабличное деление с большей точностью и достичь правильных результатов. Помните, что практика и постоянное улучшение навыков помогут вам стать опытным в этой области.



