Весовая матрица – это структура данных, играющая важную роль в области информатики. Она представляет собой таблицу, состоящую из чисел или других данных, которые описывают взаимосвязь между различными сущностями. Концепция весовой матрицы широко используется во множестве задач, включая анализ данных, машинное обучение, графовые алгоритмы и другие области.
Основная идея весовой матрицы заключается в том, что каждая ячейка таблицы содержит число, отражающее степень влияния одной сущности на другую. Например, в графовых алгоритмах весовая матрица может описывать стоимость перемещения между вершинами графа. В анализе данных весовая матрица может использоваться для оценки сходства между объектами. В машинном обучении весовая матрица часто используется для обучения моделей, где каждая ячейка представляет важность признака для предсказания.
Применение весовых матриц обладает рядом преимуществ. Они позволяют учесть различные аспекты или важности при решении задачи. Кроме того, весовые матрицы упрощают работу с данными, позволяют находить оптимальные решения и устанавливать приоритеты. Важно отметить, что весовые матрицы могут быть различной размерности и иметь разные значения в ячейках, в зависимости от конкретной задачи и области применения.
Весовая матрица: что это такое и как она работает

Весовая матрица широко применяется в различных областях, включая машинное обучение, нейронные сети и графовые алгоритмы. Она позволяет описать и анализировать сложные структуры и взаимосвязи между элементами.
Как работает весовая матрица? Каждый элемент матрицы представляет собой значение связи между соответствующими элементами. Например, в матрице смежности графа, элементы матрицы указывают наличие или отсутствие ребра между вершинами, а числа отражают вес или стоимость этой связи.
Весовая матрица обычно представляется в виде квадратной матрицы, где каждый столбец и строка соответствуют элементам. Это позволяет легко находить значение связи между элементами и выполнять операции, такие как поиск кратчайшего пути в графе.
Важно отметить, что весовая матрица может быть симметричной или асимметричной. В симметричной матрице вес связи между двумя элементами одинаков как в строке, так и в столбце. В асимметричной матрице значения могут отличаться для разных направлений связи.
Использование весовых матриц позволяет эффективно моделировать и анализировать сложные системы с множеством взаимосвязей. Они являются мощным инструментом для решения различных задач и задавания весовых значений связей между элементами.
Определение понятия "весовая матрица" в информатике

Весовая матрица широко применяется в различных областях информатики, включая алгоритмы машинного обучения, графовые алгоритмы, оптимизацию и принятие решений. Она позволяет решать задачи, связанные с поиском кратчайшего пути между вершинами графа, оптимальным распределением ресурсов или построением оптимального расписания.
Каждый элемент весовой матрицы может быть представлен числом, которое определяет степень связи между соответствующими элементами. Например, весовая матрица может быть использована для описания дистанций между городами, где значение элемента матрицы обозначает расстояние между двумя городами.
Операции над весовыми матрицами включают нахождение суммы, произведения, транспонирования и других математических операций. Весовая матрица также может быть преобразована в граф, где элементы матрицы представлены вершинами, а веса задают веса ребер графа.
Роли и применение весовых матриц в информационных системах
Весовые матрицы играют важную роль в информационных системах, обеспечивая эффективную обработку и анализ данных. Они широко применяются в различных областях, таких как машинное обучение, искусственный интеллект, биология, экономика и другие.
Главное преимущество весовых матриц заключается в их способности учитывать важность каждого элемента данных при принятии решений. Каждый элемент матрицы имеет свой вес, который отражает его значимость или вклад в общий результат.
В машинном обучении весовые матрицы широко используются для обучения моделей и классификации данных. Веса помогают оценить влияние каждого признака на результат модели, что позволяет учесть особенности и различные факторы при анализе.
Весовые матрицы также применяются для ранжирования и рекомендации. Они могут помочь определить важность и релевантность каждого элемента в большом наборе данных, что позволяет выделять наиболее подходящие и значимые результаты для конкретного запроса.
В биологии и генетике весовые матрицы используются для анализа последовательностей ДНК и определения областей, которые имеют значение для организма. Веса позволяют выявить и классифицировать определенные зоны или мотивы в геноме, что помогает в понимании естественных процессов и развитии новых исследований.
В экономике и финансах весовые матрицы используются для анализа рынка и определения рисков и возможностей. Веса могут быть назначены каждому инструменту или активу и представлять их вклад в общий индекс или портфель. Такой подход позволяет оценить и управлять рисковыми факторами и оптимизировать инвестиционные стратегии.
Весовые матрицы являются основным инструментом для обработки и анализа данных в информационных системах. Их применение в различных областях позволяет учесть разнообразные факторы и особенности данных, что способствует принятию более точных и информированных решений.
Принцип работы и расчет весовых матриц
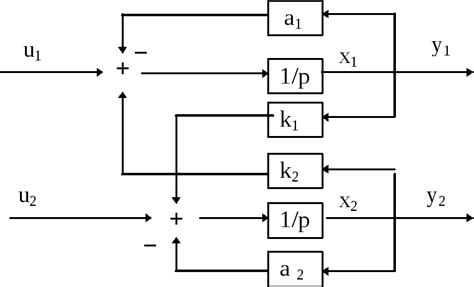
Принцип работы весовой матрицы заключается в том, что она позволяет оценить степень важности и влияния каждого элемента на другие в рамках определенной системы или задачи. Значение веса может быть положительным, отражающим положительное влияние, или отрицательным, отражающим отрицательное влияние. Весовая матрица может быть использована для решения различных задач, таких как анализ данных, классификация, прогнозирование и другие.
Расчет весовой матрицы зависит от конкретной задачи или системы, в которой она применяется. Он требует анализа и оценки взаимосвязи между элементами с использованием различных методов и алгоритмов. Вес можно определить, например, на основе статистической информации, экспертных оценок или с использованием машинного обучения.
Преимуществом использования весовых матриц является возможность более точной и объективной оценки важности каждого элемента, что позволяет принимать более информированные и эффективные решения. Однако, для достижения достоверных результатов, необходимо учитывать особенности и ограничения задачи, а также проводить регулярную проверку и обновление весовой матрицы в соответствии с изменяющимися условиями и требованиями.
| Элемент 1 | Элемент 2 | Элемент 3 | |
|---|---|---|---|
| Элемент 1 | 1 | 0.5 | -0.2 |
| Элемент 2 | -0.8 | 1 | 0.7 |
| Элемент 3 | 0.3 | -0.6 | 1 |
Приведенный выше пример показывает возможную расстановку весов для трех элементов в системе. Значение 1 обозначает положительную взаимосвязь, 0 указывает на отсутствие связи, а отрицательные значения отражают отрицательную взаимосвязь. Такая весовая матрица может быть использована, например, для классификации и прогнозирования, где важность каждого элемента будет учитываться в дальнейшем анализе и принятии решений.
Примеры использования весовых матриц в реальных проектах

Весовые матрицы широко применяются в различных областях информатики и машинного обучения. Ниже приведены несколько примеров реального использования весовых матриц:
- Обработка естественного языка (NLP): Весовые матрицы являются основным инструментом для представления текстовых данных в задачах NLP, таких как анализ тональности, классификация документов и машинный перевод. Веса отображают частоту или важность слов в тексте, позволяя алгоритмам машинного обучения сделать более точные предсказания.
- Рекомендательные системы: Весовые матрицы используются для моделирования взаимодействий между пользователями и элементами, такими как фильмы, товары или музыкальные композиции. Они помогают предсказывать предпочтения пользователей и рекомендовать им новые элементы, опираясь на сходство с другими пользователями или элементами.
- Компьютерное зрение: Весовые матрицы применяются для обработки изображений в задачах компьютерного зрения, таких как распознавание объектов, сегментация изображений и классификация. Веса могут отражать важность различных пикселей или признаков в изображении, позволяя алгоритмам выделять ключевые области и делать более точные предсказания.
Это только некоторые из множества примеров использования весовых матриц. Все они демонстрируют важность и широкий спектр применения этого инструмента в информатике и машинном обучении.



