Геометрия – это наука, изучающая пространственные фигуры и их свойства. Одним из ключевых понятий в геометрии является угол. Угол образуется при соединении двух лучей, и в его состав входят вершина и стороны. Вершина угла – это точка, в которой пересекаются два луча, образующих угол. Стороны угла – это лучи, исходящие из вершины и образующие угол.
Каждый угол имеет свои особенности и свойства. Например, сумма всех углов вокруг точки равна 360 градусам. Углы бывают острые (меньше 90 градусов), прямые (равные 90 градусов), тупые (больше 90 градусов) и полные (равные 180 градусов). Также углы могут быть равными или неравными по величине. Важно понимать, что углы могут быть представлены как в градусах, так и в радианах, и их значение зависит от контекста задачи.
Чтобы лучше понять понятия вершин и сторон углов, рассмотрим примеры. Представьте, что вы рисуете фигуру на бумаге. Каждый угол этой фигуры будет иметь свою вершину и две стороны. Например, рассмотрим квадрат – фигуру с четырьмя равными сторонами и четырьмя прямыми углами. В каждом углу квадрата есть вершина, а две стороны угла – это две стороны квадрата, пересекающиеся в вершине угла.
Определение вершин и сторон углов в геометрии
Строительные элементы угла являются его стороны. Стороны угла представляют собой две прямые линии, и каждая из них начинается от вершины и распространяется в определенном направлении. Стороны угла могут быть равными или не равными по длине, и они могут быть прямыми или кривыми.
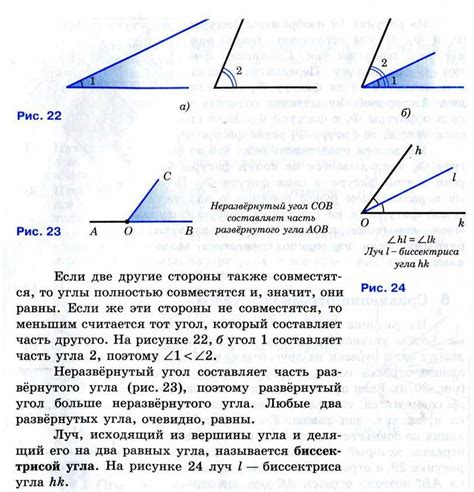
В геометрии стороны угла часто обозначаются буквами. Обычно первая буква обозначает вершину угла, а две последующие буквы обозначают стороны угла. Например, угол ABC имеет вершину в точке B и стороны AB и BC.
Вершины и стороны углов в геометрии играют важную роль при изучении свойств углов и их классификации. Знание определения вершин и сторон углов позволяет лучше понимать геометрические фигуры и использовать их в различных математических задачах и приложениях.
Понятие вершин и сторон углов

Вершина угла - точка, в которой сходятся две стороны угла. Вершина угла может быть представлена в виде точки на плоскости или на пространстве.
Углы могут иметь различное количество сторон. В зависимости от количества сторон, углы могут быть классифицированы как одноугольные (нулевой угол), двугольные (прямой угол), трехугольные (острый угол), четырехугольные (полный угол) и так далее.
Столь же важно помнить, что углы могут быть отрицательными или возвратными, если они разворачиваются в противоположных направлениях.
Структура угла включает в себя его вершину и стороны. Возможно, одна или обе стороны угла могут быть бесконечными лучами.
Каждая сторона угла, стартуя от его вершины, расширяется в определенном направлении.
Понимание понятия вершин и сторон углов является фундаментальным для изучения геометрии, так как они играют важную роль в определении свойств и классификации углов, а также в решении различных геометрических задач.
Свойства вершин и сторон углов

Вершины углов могут иметь различные свойства:
- Угол может быть остроугольным, прямым, тупоугольным или полным в зависимости от его размера.
- Два угла называются вертикальными, если они имеют общую вершину и стороны этих углов являются продолжением друг друга.
- Углы, дополняющие друг друга, называются дополнительными. Сумма двух дополнительных углов равна 180 градусам.
- Углы, смежные по стороне, называются смежными. Сумма смежных углов равна 180 градусам.
Кроме вершин, углы имеют стороны, которые соединяют вершины. Стороны углов могут также иметь свои свойства:
- Сторона угла - это отрезок прямой, который является одной из граней угла и соединяет две его вершины.
- Длины сторон углов могут быть равными или разными в зависимости от формы угла.
- Стороны примыкающих углов совпадают, если углы имеют общую сторону.
Знание свойств вершин и сторон углов помогает ученым и инженерам в решении задач, связанных с пространственными формами и конструкциями.
Примеры с вершинами и сторонами углов
В геометрии угол определяется как область между двумя лучами, которые имеют общую точку, называемую вершиной угла. Для полного определения угла необходимо указать его вершину и две стороны.
Рассмотрим несколько примеров углов:
| Пример | Вершина | Стороны |
|---|---|---|
| Прямой угол | A | AB, AC |
| Острый угол | B | BC, BA |
| Тупой угол | C | CA, CB |
| Прямоугольный угол | D | DE, DF |
В примерах выше, вершина угла обозначена буквами A, B, C и D, а стороны - парой букв (например, AB, AC). Каждый угол имеет свой тип, который зависит от величины угла и его свойств.
Знание вершин и сторон углов позволяет проводить различные геометрические конструирования и решать задачи, связанные с вычислением величины угла и его свойствами.



