Равенства и неравенства – основные математические понятия, без которых невозможно представить себе нашу жизнь. Они играют важную роль не только в математике, но и во многих других науках и практических областях. Равенство – это сравнение двух выражений, которые оказываются абсолютно одинаковыми. Вместе с тем неравенство говорит нам, что два выражения различны между собой и имеют отличные от друг друга значения.
Для математических исследований и решения задач важным является умение распознавать верные равенства и неравенства. Среди равенств следует различать истинные и ложные. Истинные равенства подтверждаются наличием множества доказательств, которые помогают увидеть и объяснить, в чем их суть. С другой стороны, ложные равенства могут создавать путаницу и вводить в заблуждение, несмотря на то, что на первый взгляд они кажутся верными.
Неравенства, в свою очередь, имеют важное значение при сравнении различных значений. Они позволяют строить порядок и определять взаимоотношения между числами и объектами. Неравенство может указывать на то, что одно значение больше или меньше другого, что один объект имеет преимущество перед другим. Все это делает неравенство необходимым инструментом для анализа и объяснения различий и отношений в разных ситуациях.
Верные равенства и неравенства: важность определения

В математике, равенства и неравенства играют важную роль. Они помогают нам устанавливать соотношения между числами и объектами, а также решать различные математические задачи.
Верное равенство означает, что две стороны уравнения имеют одно и то же значение. Например, "2 + 2 = 4" - это верное равенство, потому что обе стороны равны 4.
Определение верного неравенства также важно. Неравенство устанавливает отношение между двумя числами или объектами, указывая, что одно число больше или меньше другого. Например, "5 > 3" - это верное неравенство, потому что 5 больше 3.
Понимание верных равенств и неравенств позволяет нам проводить математические операции, решать уравнения, а также анализировать и интерпретировать данные и информацию в различных задачах и ситуациях.
Итак, определение верных равенств и неравенств является основополагающим элементом математики и имеет большое значение для выполнения математических операций, решения уравнений и принятия обоснованных решений в различных сферах нашей жизни.
Определение равенства и неравенства в математике

Равные объекты имеют одинаковое значение или идентичность. В математике это означает, что два объекта, такие как числа, переменные или выражения, представляют одну и ту же величину или значение.
Неравенство - это математическое понятие, которое гласит, что два математических объекта не равны между собой. В математике неравенство обозначается символами "<", ">", "<=" или ">=", которые читаются как "меньше", "больше", "меньше или равно" и "больше или равно" соответственно.
Неравные объекты имеют различные значения или идентичность. В математике это означает, что два объекта, такие как числа, переменные или выражения, представляют различные величины или значения.
Понимание равенства и неравенства является важным для решения математических задач и построения логических аргументов. Эти понятия широко используются в алгебре, геометрии, теории вероятностей, физике и других областях математики и науки.
Роль верных равенств и неравенств в решении уравнений
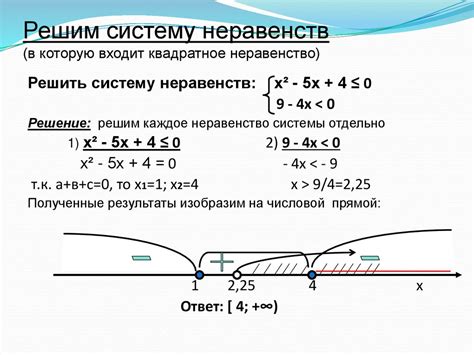
Равенства и неравенства играют важную роль в решении уравнений, так как они позволяют нам установить соответствие между двумя математическими выражениями или наборами выражений.
Основной целью решения уравнений является нахождение значений переменных или конкретного значения, при которых уравнение становится верным.
Верные равенства и неравенства помогают нам ограничить диапазон возможных значений переменных и провести анализ решений уравнения.
Например, для решения уравнения 2x + 3 = 7 мы можем использовать равенство 2x + 3 = 7, чтобы установить соответствие между выражением на левой стороне и выражением на правой стороне. Затем мы можем использовать правило, что если два выражения равны, то мы можем приравнять значения внутри скобок и решить получившееся уравнение. В данном случае, решив уравнение, мы получим значение переменной x = 2.
Однако, равенства и неравенства не всегда приводят к одному конкретному решению. В некоторых случаях, они могут давать нам диапазон возможных значений, которые удовлетворяют уравнению. Например, неравенство x > 0 означает, что значение переменной x должно быть больше нуля. В этом случае, решением неравенства будет любое число больше нуля.
| Вид равенства/неравенства | Описание | Пример | Роль в решении уравнений |
|---|---|---|---|
| Равенство | Уравнение, в котором два выражения равны друг другу | 2x + 3 = 7 | Позволяет установить соответствие между выражениями и найти конкретное значение переменной |
| Неравенство | Уравнение, в котором два выражения не равны друг другу | x > 0 | Устанавливает ограничения на диапазон возможных значений переменной или задает промежутки решений |
Таким образом, верные равенства и неравенства являются неотъемлемой частью решения уравнений, помогая нам определить допустимые значения переменных и приводя к конкретным или диапазону решений.
Значение верных равенств и неравенств в научных исследованиях

Верные равенства и неравенства в научных исследованиях могут быть использованы для:
- Описания и формулирования законов природы и физических явлений;
- Определения зависимостей между различными переменными;
- Проверки статистических гипотез и выявления значимых различий;
- Определения пределов и диапазонов изменений величин;
- Моделирования и предсказания результатов экспериментов.
Применение верных равенств и неравенств в повседневной жизни
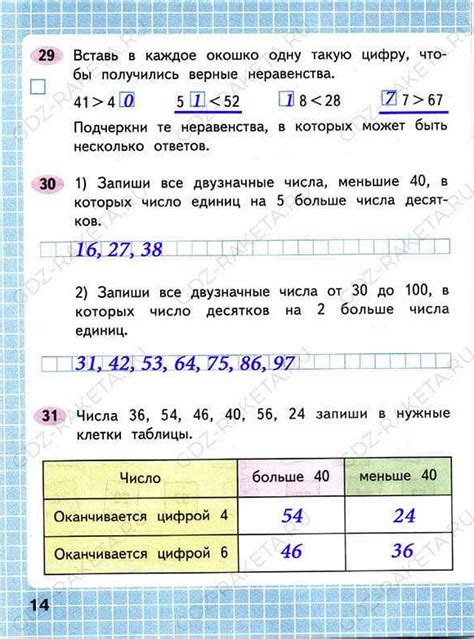
Одним из применений верных равенств и неравенств является финансовое планирование. Например, если мы хотим купить товар, то нам нужно установить, хватает ли у нас денег. Здесь мы можем использовать неравенство, чтобы сравнить стоимость товара с доступными нам средствами. Если стоимость товара меньше или равна нашим средствам, то мы можем позволить себе его покупку.
Верные равенства и неравенства также применяются в строительстве и ремонте. Например, при покупке строительных материалов необходимо учесть их стоимость и количество. Математические выражения позволяют нам определить, сколько нужно купить материалов и сколько это будет стоить.
Кроме того, равенства и неравенства играют важную роль в изучении наук, таких как физика и химия. В этих науках мы часто сталкиваемся с уравнениями, которые описывают различные законы и закономерности природы. Например, закон сохранения энергии представляется в виде уравнения, где сумма начальной и потенциальной энергии равна сумме кинетической и других видов энергии.
Таким образом, верные равенства и неравенства являются неотъемлемой частью нашей повседневной жизни. Они позволяют нам решать задачи, планировать финансы, строительство и учиться новым наукам. Использование этих математических выражений улучшает наши навыки анализа и логического мышления, что важно для успешной жизни в современном обществе.



