В геометрии существует множество различных задач на нахождение неизвестных величин в треугольниках. Одной из таких задач является нахождение длин сторон треугольника, если известны некоторые условия. В данной задаче известно, что сторона АС равна 20.
Для решения данной задачи можно использовать различные методы и формулы, включая теоремы о треугольниках. Например, можно воспользоваться теоремой Пифагора или используя теорему косинусов.
Также при решении данной задачи может быть полезным знание свойств треугольников, таких как равенство углов или сумма длин двух сторон, например, гипотенузы прямоугольного треугольника. Важно учитывать, что для решения задачи может потребоваться дополнительная информация о треугольнике, например, длины других сторон или значения углов.
Свойства треугольника АВС с АС = 20
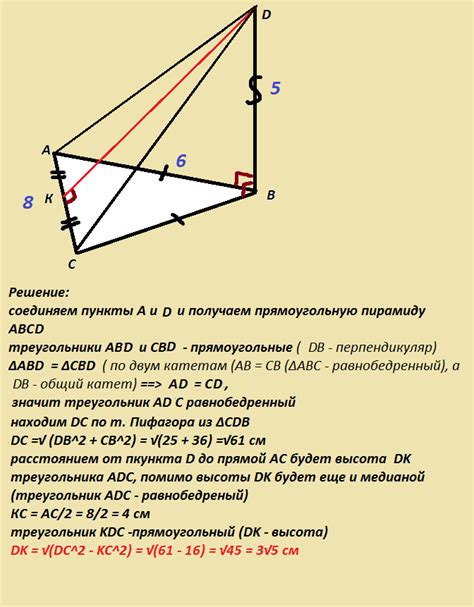
В данном треугольнике АВС известно, что сторона АС равна 20 единиц. Из этой информации можно вывести несколько свойств данного треугольника.
1. Треугольник АВС является непрямоугольным. Если бы он был прямоугольным, то сторона АС была бы гипотенузой, а так как АС ≠ √(АВ² + ВС²), то треугольник не прямоугольный.
2. Треугольник АВС может быть равнобедренным или разносторонним. Равнобедренность треугольника АВС определяется длиной его сторон. Если сторона АВ и сторона ВС также равны, то треугольник АВС является равнобедренным. В противном случае, когда все три стороны треугольника различны, он считается разносторонним.
3. Сумма длин двух сторон треугольника всегда больше длины третьей стороны, а разность длин двух его сторон всегда меньше длины третьей стороны по модулю. В данном случае, сумма длин сторон АВ и ВС равна 20+20=40, что больше длины стороны АС (20). Также разность длин сторон АВ и ВС равна 20-20=0, что меньше длины стороны АС (20).
Таким образом, треугольник АВС с АС = 20 является непрямоугольным и может быть как равнобедренным, так и разносторонним.
Определение треугольника АВС

Треугольник АВС обладает следующими свойствами:
- Треугольник имеет три стороны - АВ, ВС и СА - и три угла - А, В и С.
- Сумма всех внутренних углов треугольника равна 180 градусам.
- Сторона треугольника является отрезком, соединяющим две его вершины.
- Вершина треугольника - это его конечная точка.
- Высота треугольника - это отрезок, опущенный из вершины треугольника на противоположную сторону или ее продолжение.
- Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
- Биссектриса треугольника - это отрезок, разбивающий угол треугольника на два равных угла.
- Окружность, описанная около треугольника (описанная окружность), проходит через все вершины треугольника.
- Вписанная окружность треугольника (вписанная окружность) касается всех сторон треугольника.
Зная длину отрезка АС равную 20 единицам, можно использовать различные геометрические методы для нахождения других параметров треугольника, таких как длины других сторон, значения углов, площадь и периметр.
Равенство сторон треугольника АВС
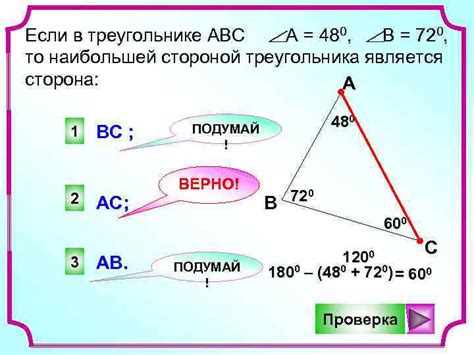
В треугольнике АВС известно, что сторона АС равна 20. Давайте рассмотрим, как это равенство влияет на остальные стороны треугольника.
Для начала, вспомним основной принцип равенства сторон треугольника: если две стороны треугольника равны, то соответствующие им углы также равны. Таким образом, если сторона АС равна 20, то сторона СА также равна 20.
Исходя из этого равенства, получаем, что треугольник АВС является равнобедренным. Это значит, что сторона АВ равна стороне ВС.
Можно также заметить, что сторона АВ равна сумме сторон АС и СВ. Так как АС равна 20, получаем, что АВ равна 20 + ВС. Из этого равенства можно найти длину стороны ВС, если известна длина стороны АВ.
| Сторона | Длина |
|---|---|
| СА | 20 |
| АВ | 20 |
| ВС | ? |
Таким образом, равенство сторон треугольника АВС, в частности, равенство сторон АС и СА, имеет важное значение для определения его геометрических и угловых свойств.
Соотношения длин сторон треугольника АВС

В данном треугольнике АВС с известной длиной стороны АС, равной 20, мы можем вывести несколько интересных соотношений с длинами других сторон.
- Согласно неравенству треугольника, сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Таким образом, мы можем указать неравенства: АВ + ВС > АС, АВ + АС > ВС, ВС + АС > АВ.
- С помощью теоремы Пифагора, мы можем выразить длину стороны АВ через стороны АС и ВС: х = √(АС^2 - у^2).
- Используя такое же уравнение для стороны ВС, мы можем найти длину стороны АВ: у = √(АС^2 - х^2).
Таким образом, зная длину одной из сторон треугольника и имея указанные неравенства, мы можем определить допустимый диапазон значений для длин остальных сторон. Это позволяет нам лучше понять и визуализировать геометрические особенности треугольника АВС.
Углы треугольника АВС
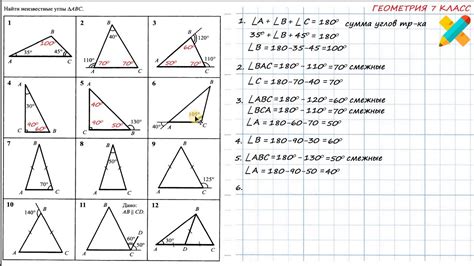
В треугольнике АВС известно, что АС равно 20. Чтобы рассмотреть углы этого треугольника, мы можем использовать различные методы, например, теорему синусов или теорему косинусов.
Теорема синусов гласит, что отношение длины стороны к синусу противолежащего угла одинаково для всех сторон треугольника. Таким образом, мы можем использовать эту теорему для нахождения углов треугольника АВС.
Теорема косинусов позволяет найти один из углов треугольника, если известны длины всех его сторон. Она утверждает, что квадрат любой стороны равен сумме квадратов остальных двух сторон, умноженной на два произведения этих сторон и косинуса противолежащего угла.
Известная длина стороны АС позволяет нам использовать теорему косинусов для нахождения углов треугольника АВС. Путь мы обозначим угол между сторонами АВ и АС как α. Тогда у нас есть следующее уравнение:
AC^2 = AB^2 + BC^2 - 2 * AB * BC * cos(α)
В нашем случае мы знаем, что АС равно 20. Это позволяет нам решить уравнение и найти значение угла α. Зная один угол, мы можем найти остальные два угла, используя свойства треугольника, например, что сумма всех углов в треугольнике равна 180 градусам.
Последствия равенства сторон треугольника АВС

Когда сторона АС треугольника АВС равна 20, возникает несколько интересных последствий.
Во-первых, равные стороны АС и АВ указывают на равность углов при основании треугольника. Это замечательное свойство позволяет нам сразу утверждать, что угол А равен углу В.
Во-вторых, равенство сторон можно использовать для нахождения других сторон и углов треугольника. Например, если известна длина стороны АВ (пусть это также равно 20), то по теореме Пифагора мы можем найти длину стороны BC. Если известен угол А (равный углу В), то мы можем использовать тригонометрические соотношения для нахождения других сторон и углов.
Наконец, равенство сторон АС и АВ может быть использовано для классификации треугольника. При равных сторонах треугольник АВС является равносторонним, а это означает, что все его стороны равны, а все его углы равны 60 градусам.
| Последствия равенства сторон АС и АВ: |
|---|
| 1. Равенство углов А и В при основании треугольника |
| 2. Возможность нахождения других сторон и углов треугольника |
| 3. Классификация треугольника как равностороннего |



