Узел – это одно из основных понятий в математике, которое изучают в 5 классе. Узел может быть представлен в виде точки, которая может быть связана с другими точками или объектами. В математике узел используется для представления связей между объектами.
В 5 классе дети учатся работать с узлами, решая различные задачи. Например, они могут использовать узлы для представления графов, которые позволяют визуально отобразить связи между объектами. Узлы могут быть соединены линиями, которые представляют отношения или зависимости между объектами.
Использование узлов помогает детям развивать навыки анализа и логического мышления. Они учатся исследовать свойства узлов и отношения между ними, а также решать задачи, связанные с узлами. Например, дети могут разбираться в том, как представить план действий с помощью узлов и как определить наиболее эффективный путь или последовательность действий.
Узел в математике: определение и примеры
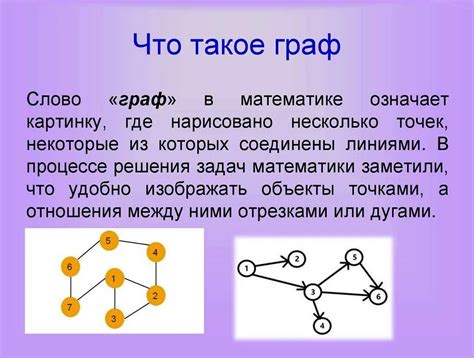
Приведем несколько примеров понятия узел в математике:
- В треугольнике АВС точки А, В и С являются узлами, так как три отрезка АВ, ВС и СА сходятся в этих точках.
- В графе точки, представляющие конечные состояния или переходы, называются узлами. Эти узлы соединены ребрами, представляющими возможные переходы между состояниями.
- В плоской фигуре, например, круге, центр является узлом, так как все линии, исходящие из данной точки, радиальные.
Узлы имеют важное значение в различных областях математики и связанных с ней наук. Они помогают нам понять структуру и связи между объектами и фигурами. Узлы также используются в алгоритмах, сетях и топологии.
Определение и свойства узла в математике

Свойства узлов в математике могут быть разнообразными. Один из основных вопросов, касающихся узлов, заключается в их различности. Например, узлы могут быть простыми или сложными, в зависимости от числа пересекаемых линий.
Узлы также могут иметь различное число пересечений. Некоторые узлы могут быть безошибочно различимы, в то время как другие могут быть изоморфными. Изучение свойств узлов позволяет углубить понимание геометрических и алгебраических закономерностей в математике.
Узлы имеют множество применений в различных областях науки и инженерии. Они используются, например, для анализа сетей, моделирования процессов, обработки изображений и многих других приложениях.
Как вычислить значение узла?

Для вычисления значения узла необходимо учитывать его тип и заданные значением приоритеты. Во-первых, нужно определить, что за операция выполняется в узле: сложение, вычитание, умножение или деление. Кроме того, если речь идет о математическом выражении с несколькими операциями, важно учесть приоритет операций, заданный в предложенном выражении.
Если узел представляет собой число, его значение считается известным и может быть использовано для дальнейших вычислений. В случае, если узел является операцией, значение узла определяется путем применения этой операции к двум или более значениям, расположенным ниже по дереву выражения.
Важно также помнить о порядке выполнения операций: сначала выполняются узлы с более высоким приоритетом, а затем с более низким. Например, узел с операцией умножения имеет более высокий приоритет, чем узел с операцией сложения, поэтому сначала выполняется умножение, а затем сложение.
Для более сложных выражений с несколькими узлами и операциями нужно последовательно вычислять значения узлов, начиная с самых верхних узлов и двигаясь вниз по дереву выражения. При этом результаты вычислений сохраняются и используются в следующих операциях.
Таким образом, вычисление значения узла в математическом выражении зависит от его типа, операции в узле и приоритета операций в выражении.
Узел как элемент графа
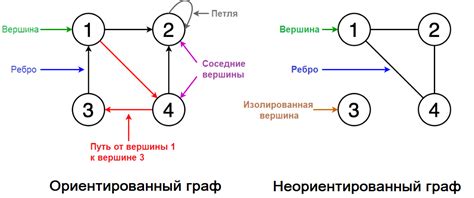
Узлы могут быть связаны друг с другом ребрами, создавая различные взаимосвязи и отношения между объектами. Каждый узел может иметь любое количество ребер, в зависимости от его роли и связей с другими узлами.
Узлы графа могут быть отмечены определенной информацией, например, названием, числовым значением или другими характеристиками. Эта информация может представлять дополнительные сведения об объекте, который представляет узел.
Графы и узлы широко используются в различных областях, включая математику, компьютерные науки, социальные сети и многое другое. Концепция узлов и графов позволяет анализировать сложные системы, выявлять взаимосвязи и понимать структуру данных. Понимание узлов и их роли в графе помогает решать задачи и исследовать различные аспекты объектов и их взаимодействия.
Типы узлов в математике
Существует несколько типов узлов в математике:
- Входной узел: это узел, через который данные поступают в систему. Он обозначается стрелкой, направленной к узлу. Входной узел может принимать различные значения в зависимости от входных данных.
- Выходной узел: это узел, через который данные покидают систему. Он обозначается стрелкой, направленной из узла. Выходной узел может иметь различное значение в зависимости от обработки данных в системе.
- Промежуточный узел: это узел, который находится между входными и выходными узлами и выполняет определенную функцию или обрабатывает данные. Промежуточные узлы могут быть представлены различными математическими операциями или условными операторами.
- Узел решения: это узел, который представляет собой конечный результат или решение задачи. Он может быть выходным узлом или узлом, от которого исходят другие узлы.
- Соединительный узел: это узел, который связывает два или более узлов вместе. Он может быть использован для объединения данных или передачи информации между различными узлами.
Типы узлов в математике могут варьировать в зависимости от конкретной задачи или модели. Понимание различных типов узлов поможет лучше понять структуру и связи между узлами в математической модели.
Примеры задач с узлами в математике для 5 класса

- Задача 1: На графике изображены узлы, соответствующие температуре воздуха каждый день за неделю. В понедельник температура была -2 градуса, во вторник -1 градус, в среду 0 градусов, в четверг 1 градус, в пятницу 2 градуса, в субботу -3 градуса и в воскресенье -4 градуса. Какая температура была в среду?
- Задача 2: На графике изображены узлы, соответствующие количеству собранных яблок каждый день на протяжении недели. Узел в понедельник - 3 яблока, узел во вторник - 5 яблок, узел в среду - 2 яблока, узел в четверг - 4 яблока, узел в пятницу - 6 яблок, узел в субботу - 1 яблоко и узел в воскресенье - 2 яблока. Сколько яблок было собрано за всю неделю?
- Задача 3: На графике изображены узлы, соответствующие росту растения каждую неделю. Узел в первую неделю - 10 см, узел во вторую неделю - 12 см, узел в третью неделю - 15 см, узел в четвертую неделю - 18 см, узел в пятую неделю - 20 см. На сколько сантиметров выросло растение за 5 недель?
Задачи с узлами помогают развить навыки анализа графиков и визуализации информации. Они требуют внимательности и логического мышления для правильного решения. Попробуйте решить данные задачи с узлами, чтобы лучше понять их использование в математике.



