Уравнение - это математическое выражение, в котором через знак равенства связаны две алгебраические функции или выражения. К примеру, уравнение может иметь вид 3x + 5 = 10, где x - неизвестное значение, а числа 3, 5 и 10 - известные значения или коэффициенты. Часто при решении уравнений мы ищем значение неизвестной величины, которое удовлетворяет данному уравнению.
Однако, в некоторых случаях уравнение может не иметь корней, то есть не существует такого значения неизвестной величины, которое было бы решением данного уравнения. Уравнение без корней может возникать по разным причинам и иметь свое значение в различных областях науки и практики.
Одна из причин, по которой уравнение может не иметь корней - это наличие противоречащих условий. Например, если уравнение содержит два равенства, которые являются противоречивыми, то такое уравнение будет несовместным и не будет иметь корней. Это может быть важно в области систем уравнений, где необходимо найти решение для нескольких переменных, учитывая все заданные условия и ограничения.
Уравнение без корней: что это такое?

Однако, существуют уравнения, которые не имеют решений. Это может произойти по разным причинам:
- Первая причина - противоречие в уравнении. Например, если уравнение содержит противоречивые утверждения, такие как "2 = 4" или "0 = 1", то такое уравнение не имеет решений.
- Вторая причина - неправильно поставленная задача. В определенных случаях уравнения могут быть сформулированы некорректно, что приводит к отсутствию решений. Например, уравнение с отрицательным корнем в квадратном корне может не иметь решения, если речь идет о решении в действительных числах.
Возможные причины отсутствия корней в уравнении

Отсутствие корней в уравнении может иметь различные причины. Изучение этих причин позволяет более глубоко разобраться в сути уравнений и их решений.
Одной из возможных причин отсутствия корней является нерациональность уравнения. Если уравнение содержит иррациональные числа, например, корень квадратный из отрицательного числа, то оно не имеет решений в области действительных чисел. Однако, в комплексной плоскости уравнение может иметь решения.
Другой причиной отсутствия корней может быть нарушение условий решаемости уравнения. Например, квадратное уравнение может не иметь корней, если дискриминант меньше нуля. В этом случае его решения тоже можно найти в комплексной плоскости.
Также отсутствие корней может быть связано с тем, что уравнение не имеет смысла в рассматриваемой системе. Например, уравнение может описывать отрицательные значения в условиях, когда только положительные значения имеют физический смысл.
| Причина | Значение |
|---|---|
| Иррациональность уравнения | Уравнение содержит иррациональные числа |
| Нарушение условий решаемости | Дискриминант квадратного уравнения меньше нуля |
| Отсутствие физического смысла | Уравнение описывает нереальные значения |
Несовместность уравнения с вводными данными
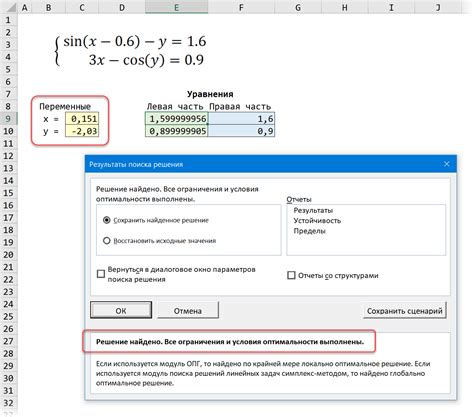
При решении математических задач часто возникает ситуация, когда уравнение не имеет корней. Это означает, что вводные данные не удовлетворяют условиям уравнения и не позволяют найти его решение.
Несовместность уравнения может возникнуть из-за различных причин. Одна из них – нарушение условий задачи. Например, если в задаче о длине стороны треугольника указано, что она должна быть больше нуля, то уравнение, которое задает это условие, становится несовместным при отрицательных значениях этой стороны.
Другой причиной несовместности уравнения может быть противоречие между вводными данными. Например, если в уравнении задано, что сумма двух чисел должна быть равна 10, а в условии задачи указано, что одно из этих чисел должно быть меньше 5, то уравнение не имеет решения.
Несовместность уравнения означает, что задача не может быть решена в рамках заданных условий. В таком случае необходимо пересмотреть условия задачи и вводные данные, чтобы найти ошибку или противоречие. Если это не удается, возможно, задача имеет некорректную постановку или неправильное решение.
При работе с несовместным уравнением важно быть внимательным и внимательно анализировать вводные данные. Иногда ошибки могут быть незначительными и их можно исправить, чтобы получить совместное уравнение и найти его решение.
Таким образом, несовместность уравнения с вводными данными указывает на противоречие или ошибку в условии задачи. Решение такой задачи требует внимательного анализа и пересмотра вводных данных, чтобы найти причину несовместности и исправить ее.
Присутствие комплексных или мнимых корней

Уравнение может не иметь решений в вещественных числах, но иметь комплексные или мнимые корни. Это означает, что ответ на уравнение можно найти только в комплексной числовой системе.
Комплексные числа состоят из вещественной и мнимой частей и обозначаются в виде \(a + bi\), где \(a\) - вещественная часть, а \(b\) - мнимая часть.
Мнимые числа обозначаются вида \(bi\) и являются частным случаем комплексного числа, где \(a\) равно 0.
Комплексные корни уравнения могут быть представлены в виде \(x = a + bi\), где \(a\) и \(b\) - вещественные числа.
Присутствие комплексных или мнимых корней в уравнении означает, что его график не пересекает ось абсцисс на вещественных числах. Однако, на комплексной плоскости, где ось абсцисс соответствует вещественным числам, уравнение может иметь точки пересечения.
Комплексные корни могут иметь важное значение в различных областях, таких как физика, электротехника, и теория вероятностей. Они могут представлять значения переменных, которые не могут быть выражены в вещественных числах, или быть решением сложных математических моделей.
Зависимость уравнения от константных параметров

Уравнение без корней может зависеть от различных константных параметров. Константы могут влиять на форму и распространение уравнения, а также на его физический и геометрический смысл.
Константы могут изменяться в зависимости от условий задачи или физической системы. Изменение констант может привести к появлению или исчезновению корней уравнения.
Например, рассмотрим уравнение квадратного трехчлена ax2 + bx + c = 0. Здесь константы a, b и c влияют на форму и распространение уравнения, а также на наличие корней. Если a = 0, то уравнение становится линейным, а значение b = 0 может привести к одному корню.
Константные параметры также могут определять физический смысл уравнения. Например, в уравнении движения тела под воздействием силы тяжести mа = mg, где m - масса, a - ускорение, g - ускорение свободного падения, константы m и g определяют зависимость уравнения от параметров массы тела и ускорения свободного падения.
Таким образом, константные параметры играют важную роль в уравнениях без корней и могут определять их свойства и смысл. Изменение этих параметров может изменить характеристики уравнения и его решений.
Значение и применение уравнений без корней

Значение уравнений без корней связано с понятием неразрешимости. Если уравнение не имеет решений, это может указывать на некоторые особенности или ограничения системы или модели, описываемой уравнением.
Одно из применений уравнений без корней в математике - изучение алгебраических структур. Например, в теории кольца уравнение без корней может свидетельствовать о свойствах кольца или его элементов.
В физике уравнения без корней могут возникать при моделировании сложных систем или при решении задач с ограничениями. Они могут указывать на невозможность получения физического решения и требовать изменения модели или постановки задачи.
В экономике и финансах уравнения без корней могут возникать при анализе рынков или определении равновесия. Неразрешимость уравнений может указывать на отсутствие равновесия или неустойчивость системы.
Кроме того, уравнения без корней могут иметь важное значение в теоретическом исследовании. Они могут быть связаны с проблемами разрешимости или сложности вычислений, что открывает новые горизонты для математических исследований.
Уравнения без корней в математической физике

Одной из причин возникновения уравнений без корней может быть неправильная постановка задачи. Например, если уравнение содержит условия, которые противоречат друг другу, то оно не будет иметь решений. Это может происходить, когда задача описывает невозможные физические процессы или нарушает законы сохранения энергии, импульса и т.д.
Другой причиной может быть ограничение области определения. Математические модели часто имеют ограничения на значения переменных или параметров. Если уравнение нарушает эти ограничения, то оно может оказаться безрешимым в данной области.
Значение уравнений без корней заключается в том, что они могут указывать на ошибки в моделях или подходах к решению задач. Изучение таких уравнений позволяет лучше понять природу физических процессов и развивать новые методы и подходы к их решению.
Роль уравнений без корней в инженерных расчетах

Уравнения без корней играют важную роль в инженерных расчетах, хотя может показаться, что они не имеют практической ценности. В инженерии уравнения без корней возникают, когда необходимые условия для наличия решений не выполняются, например, из-за некорректных данных или неправильно поставленной задачи.
Одним из примеров таких уравнений является уравнение, описывающее вихреобразование в турбомашинах. Оно не имеет решений, если параметры турбины заданы неправильно или физические условия нарушены. Понимание поведения таких уравнений без корней помогает инженерам определить границы допустимых значений параметров и предотвратить возможные аварийные ситуации.
Кроме того, уравнения без корней также встречаются при моделировании сложных систем, например, при расчете течения жидкости в трубопроводе с неоднородной структурой. В таких случаях уравнение описывает физические процессы, но не имеет решений из-за сложности и нелинейности системы. Понимание этого позволяет инженерам учесть такие эффекты при проектировании системы и получить более точные результаты.
Таким образом, уравнения без корней играют важную роль в инженерных расчетах, помогая инженерам предотвратить непредвиденные ситуации, определить границы допустимых значений и учесть сложные эффекты при моделировании системы. Несмотря на то, что такие уравнения не имеют решений, их анализ и понимание являются неотъемлемой частью инженерного процесса.



