Упрощение выражений со степенями является важным элементом в алгебре и математике в целом. Это позволяет упростить сложные выражения, сделать их более понятными и легкими для работы. Однако, упрощение выражений со степенями, имеющими разные основания, может быть вызовом для многих студентов. В этой статье мы разберем несколько методов, которые помогут вам упростить такие выражения и справиться с этим вызовом.
Первым шагом в упрощении выражений со степенями с разными основаниями является поиск общего основания. Если у вас есть два или более выражений с разными основаниями, вы можете попробовать найти общее основание и привести выражения к одной форме. Например, если у вас имеется выражение "4^2" и "2^3", вы можете привести их к общей форме, возводя в степень основание 2. Таким образом, "4^2" станет "2^4", а "2^3" станет "2^3". Теперь у вас есть два выражения с одинаковыми основаниями, и их можно объединить или упростить дальше.
Если найти общее основание не удается, вы можете использовать алгебраические свойства для упрощения выражений со степенями с разными основаниями. Например, если у вас есть выражение "2^3 * 3^2", вы можете использовать свойство перемножения степеней с одинаковым основанием. В этом случае, вы можете перемножить степени и оставить одинаковое основание: "2^3 * 3^2" станет "2^3 * 9". Теперь у вас есть выражение с одним основанием, и вы можете продолжить упрощение.
Что такое степень и степенные выражения

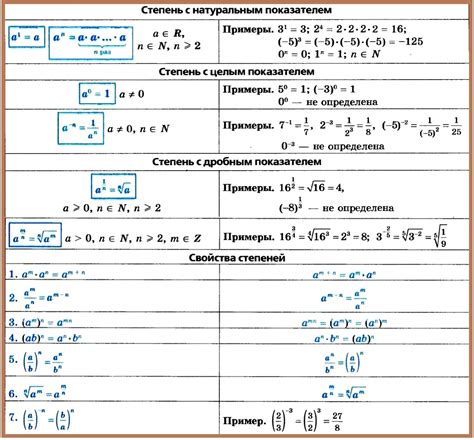
Степенным выражением называется математическое выражение, в котором присутствует степень. Оно состоит из основания, показателя степени и знака степени. Например, выражение 3^2 означает, что число 3 возведено во вторую степень. Результат этого выражения равен 9.
Степенные выражения могут иметь разные основания и показатели степени. Например, выражение 2^3 * 5^2 означает, что число 2 возведено в третью степень, а число 5 возведено во вторую степень. Результат этого выражения можно получить, умножив 2 в степени 3 на 5 в степени 2: 2^3 * 5^2 = 8 * 25 = 200.
Для упрощения степенных выражений со степенями с разными основаниями можно использовать правила алгебры. Например, если в выражении присутствуют одинаковые основания чисел с разными показателями степеней, то такие выражения можно упростить, складывая или вычитая показатели степеней. Например, выражение 2^3 * 2^4 можно упростить, складывая показатели степеней: 2^3 * 2^4 = 2^(3+4) = 2^7.
| Пример | Результат |
|---|---|
| 2^3 * 2^4 | 2^7 |
| 3^2 * 3^3 | 3^5 |
| 5^4 / 5^2 | 5^2 |
Упрощение степенных выражений позволяет упростить расчеты и сократить запись выражений, делая их более компактными и удобочитаемыми.
Понятие степени и основания
В математике наиболее распространены степени с целыми числами. Например, 2^3 означает, что число 2 возводится в третью степень. В этом случае основание составляет число 2, а степень равна 3.
В случае степени с дробными числами, основание может быть любым числом, а степень выражается в виде десятичной дроби. Например, 4^(1/2) означает, что число 4 возводится в степень, равную корню квадратному из 4. В этом случае основание составляет число 4, а степень равна 1/2.
При работе с выражениями со степенями с разными основаниями необходимо учитывать, что операции можно производить только с теми степенями, у которых основания совпадают. В противном случае выражение считается сложным и требует упрощения. Однако, если основания степеней совпадают, можно складывать или вычитать только степени, оставляя основание неизменным. Например, 2^3 + 2^4 можно упростить как 2^3 * (1 + 2), так как основания степеней совпадают и мы можем складывать только степени.
Свойства степеней с одинаковыми основаниями

Выражения со степенями с одинаковыми основаниями имеют некоторые особенности, которые помогают упростить их:
- При умножении степени с одним и тем же основанием и разными показателями степени, показатели складываются: am × an = am+n.
- При делении степени с одним и тем же основанием и разными показателями степени, показатели вычитаются: am ÷ an = am-n.
- При возведении степени с одним и тем же основанием в степень, показатели степени умножаются: (am)n = am×n.
- При умножении степеней с одинаковыми основаниями и одинаковыми показателями степени, эти степени можно складывать: am × bm = (a × b)m.
- При делении степеней с одинаковыми основаниями и одинаковыми показателями степени, эти степени можно делить: am ÷ bm = (a ÷ b)m.
- При возведении в степень произведения, можно возвести в степень каждый из множителей и перемножить полученные степени: (a × b)m = am × bm.
- При возведении в степень частного, можно возвести в степень числитель и знаменатель отдельно и разделить полученные степени: (a ÷ b)m = am ÷ bm.
Использование этих свойств позволяет значительно упростить выражения со степенями с одинаковыми основаниями и повысить эффективность работы с ними.
Свойства степеней с разными основаниями

Степени с разными основаниями можно упростить, применяя несколько свойств алгебры. Вот некоторые из них:
- Свойство умножения с одинаковыми основаниями: если у вас есть степени с одинаковыми основаниями, вы можете сложить их показатели для получения новой степени с тем же основанием. Например,
23 * 24 = 27
- Свойство деления с одинаковыми основаниями: если у вас есть степени с одинаковыми основаниями, вы можете вычесть их показатели для получения новой степени с тем же основанием. Например,
56 / 53 = 53
- Свойство возведения степени в степень: при возведении степени в степень необходимо умножить показатели степеней. Например,
(32)4 = 38
- Свойство произведения степеней с одинаковыми показателями: при перемножении степеней с одинаковыми показателями нужно умножить их основания. Например,
23 * 33 = (2 * 3)3 = 63
- Свойство частного степеней с одинаковыми показателями: при делении степеней с одинаковыми показателями нужно разделить их основания. Например,
45 / 25 = (4 / 2)5 = 25
Используя эти свойства, вы можете значительно упростить выражения со степенями с разными основаниями и сделать их более понятными и легкими для работы.
Способы упрощения степенных выражений

Упрощение степенных выражений с разными основаниями может быть сложной задачей, но существуют несколько способов сделать это проще.
1. Представление степенных выражений в виде произведения.
Если в выражении есть несколько слагаемых с одинаковыми основаниями, их можно представить в виде произведения, используя правило произведения степеней с одинаковыми основаниями:
аm * аn = а(m + n)
Например, выражение 23 * 22 можно упростить следующим образом:
23 * 22 = 2(3 + 2) = 25
2. Приведение степенных выражений к общему основанию.
Если в выражении есть слагаемые с разными основаниями, их можно привести к общему основанию, используя следующие правила:
an * bn = (a * b)n
an / am = a(n - m)
Например, выражение 23 * 33 можно упростить следующим образом:
23 * 33 = (2 * 3)3 = 63
3. Использование правила отрицательной степени.
Если в выражении есть отрицательная степень, ее можно привести к положительной степени, используя следующее правило:
a-n = 1 / an
Например, выражение 2-3 можно упростить следующим образом:
2-3 = 1 / 23 = 1 / 8
С помощью этих способов упрощения степенных выражений с разными основаниями можно значительно упростить вычисления и получить более компактные формы записи.



