Умножение чисел — как изменяются степени и как это влияет на результат

Одним из основных математических операций является умножение. Чтобы умножить два числа, нужно одно число взять несколько раз и сложить результаты. Однако, когда мы умножаем два числа со степенями, возникает вопрос: как быть с степенями? Что происходит согласно законам алгебры?

Чтобы разобраться в этом вопросе, рассмотрим пример. Пусть у нас есть число a в степени m и число b в степени n. Если умножить эти два числа, мы будем иметь a в степени m умноженное на b в степени n.

Если степени совпадают, то при умножении чисел мы придем к еще одной степени. То есть, a в степени m умноженное на b в степени m будет равно (a * b) в степени m.

Пример:

Пусть a = 2, m = 3, b = 4 и n = 2. Умножим числа: (2 в степени 3) * (4 в степени 2). Получим: (2 * 4) в степени 3, то есть 8 в степени 3. Результатом будет число 512.

Теперь разберемся, что происходит с числами, если степени отличаются. Если у нас есть a в степени m и b в степени n и меньшая степень равна 0, тогда при умножении получаем (a * b) в степени большей степени.

Пример:

Пусть a = 3, m = 4, b = 2 и n = 0. Умножим числа: (3 в степени 4) * (2 в степени 0). Получим: (3 * 2) в степени 4, то есть 6 в степени 4. Результатом будет число 1296.

Теперь, когда мы понимаем, что происходит со степенями при умножении чисел, мы можем использовать эти знания для решения задач и применения в реальной жизни.

Изучаем свойства степеней и их использование

Степени имеют определенные свойства, которые помогают упростить их вычисление:

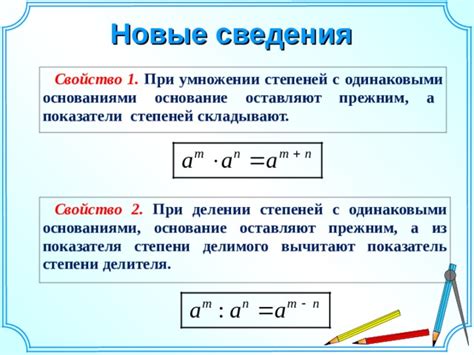
1. Свойство умножения степеней с одинаковыми основаниями позволяет перемножить две степени с одинаковыми основаниями, складывая их показатели степеней. Например, 2³ * 2⁴ = 2⁷ = 128. Таким образом, умножение степеней с одинаковыми основаниями сводится к сложению их показателей.
2. Свойство деления степеней с одинаковыми основаниями позволяет разделить две степени с одинаковыми основаниями, вычитая из показателя делителя показатель делимого. Например, 3⁵ / 3² = 3³ = 27. Таким образом, деление степеней с одинаковыми основаниями сводится к вычитанию их показателей.
3. Свойство возведения степени в степень позволяет возвести степень в еще одну степень, перемножая их показатели. Например, (2³)⁴ = 2¹² = 4096. Таким образом, возведение степени в степень сводится к перемножению их показателей.
4. Свойство возведения числа в степень 0 говорит о том, что любое число, кроме нуля, возводимое в степень 0, будет равно 1. Например, 5⁰ = 1.

Знание свойств степеней позволяет более легко и быстро выполнять арифметические операции с числами, а также применять их на практике для решения различных задач и заданий.

Например, при расчете процентов, вычислении сложных финансовых формул или изучении закономерностей в науке и природе мы используем степени чисел для упрощения и описания сложных математических и физических процессов.

Таким образом, знание свойств степеней позволяет лучше понимать и использовать математические концепции и операции в повседневной жизни и профессиональной деятельности.

Примеры умножения степеней с одинаковой степенью

Умножение чисел в степенной форме с одинаковой степенью происходит следующим образом:

• Если числа имеют одну и ту же основу, то степень складывается. Например, 2³ * 2⁴ = 2⁷, так как основа у обоих чисел равна 2, а степени 3 и 4 складываются и получается степень 7.
• Если числа имеют разные основы, но одинаковые степени, то основы перемножаются. Например, 3² * 4² = 12², так как степени у обоих чисел равны 2, а основы 3 и 4 перемножаются и получается основа 12 при степени 2.

Эти примеры демонстрируют, что умножение степеней с одинаковой степенью основано на алгоритме сложения степеней или перемножении основ, что упрощает вычисления.

Примеры умножения степеней с разными степенями

При умножении чисел со степенями важно помнить, что степени складываются. Рассмотрим несколько примеров:

Пример 1: Умножим число 2 в степени 3 на число 2 в степени 4. Получим:

2³ * 2⁴ = 2⁷ = 128

Пример 2: Умножим число 5 в степени 2 на число 5 в степени 3. Получим:

5² * 5³ = 5⁵ = 3125

Пример 3: Умножим число 10 в степени 2 на число 10 в степени 0. Получим:

10² * 10⁰ = 10²⁺⁰ = 10² = 100

Таким образом, в результате умножения чисел со степенями мы складываем степени и получаем новую степень.

Изучаем свойства степеней с отрицательными показателями

1. Знаменатель исчезает.

Если число возведено в отрицательную степень, то в результате получится число, записанное в знаменателе:

$$a^{-n} = \frac{1}{a^n}$$

Например:

$$2^{-3} = \frac{1}{2^3} = \frac{1}{8}$$

2. Число с отрицательной степенью изменяет знак.

Если число с отрицательным показателем возведено в нечетную степень, то его результат будет отрицательным:

$$a^{-n} = -a^n$$

Например:

$$(-5)^{-2} = -(-5)^2 = -25$$

3. Число с отрицательной степенью в знаменателе передвигается в числитель с положительным показателем.

Если число с отрицательной степенью находится в знаменателе, то оно перейдет в числитель с положительным показателем:

$$\frac{1}{a^{-n}} = a^n$$

Например:

$$\frac{1}{(-3)^{-4}} = (-3)^4 = 81$$

Изучение свойств степеней с отрицательными показателями позволит более глубоко понять работу с числами в алгебре и применять их в различных задачах и уравнениях.

Примеры умножения степеней с отрицательными показателями

Умножение степеней с отрицательными показателями можно производить, используя правила действий со степенями.

Если число возводится в отрицательную степень, то стоит помнить, что результат будет обратным числу, возведенному в положительную степень.

Например:

2^-3 * 2^-2

Раскроем степени:

(1/2³) * (1/2²)

Сократим дроби:

(1/8) * (1/4)

Умножим числители и знаменатели:

1/32

Итак, 2^-3 * 2^-2 = 1/32.

Аналогично, если числа с отрицательными показателями имеют разные основания, то мы можем применять те же правила.

Например:

3^-2 * 5^-1

Раскроем степени:

(1/3²) * (1/5¹)

Сократим дроби:

(1/9) * (1/5)

Умножим числители и знаменатели:

1/45

Итак, 3^-2 * 5^-1 = 1/45.

Важно помнить, что при умножении степеней с отрицательными показателями мы можем использовать правила действий со степенями и приводить числа к общему основанию.