Равнобедренный треугольник – это особый вид треугольника, который имеет две равные стороны и два равных угла.
Одна из самых важных характеристик равнобедренного треугольника - это угол при основании. Угол при основании – это один из двух углов, смежных с основанием треугольника.
Если провести перпендикуляр из вершины угла при основании к основанию, то получится высота треугольника. Заметим, что высота равнобедренного треугольника делит его на два равных прямоугольных треугольника.
Особенность угла при основании состоит в том, что он всегда меньше двух других углов треугольника.
Значение угла в равнобедренном треугольнике
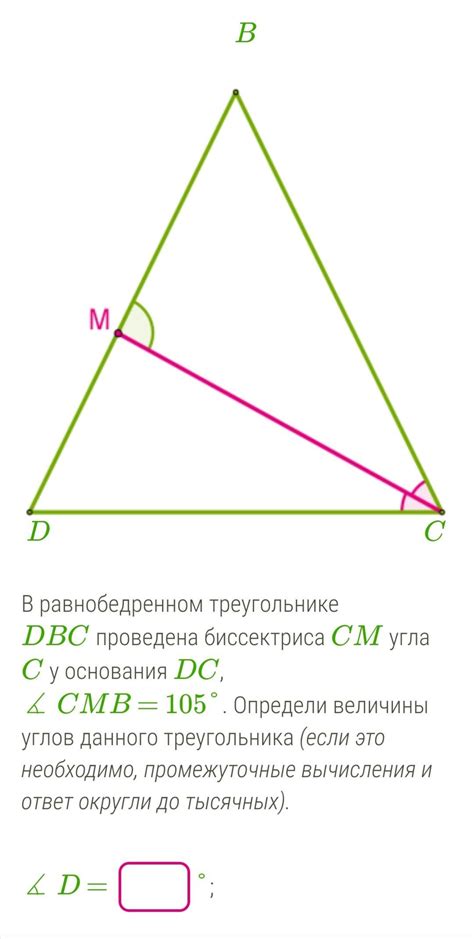
Значение угла при основании равнобедренного треугольника можно определить с помощью свойств равнобедренности треугольника:
| Свойство равнобедренности: | Два угла при основании равны | Угол при вершине равен |
| Значение угла: | $$\frac{{180^\circ - \text{{значение угла при вершине}}}}{2}$$ | $$\frac{{180^\circ - \text{{значение угла при основании}}}}{2}$$ |
Таким образом, чтобы найти значение угла при основании равнобедренного треугольника, необходимо вычесть из 180 градусов значение угла при вершине и разделить полученный результат на 2.
Зная значение угла при основании, можно проводить различные вычисления и решать задачи, связанные с равнобедренными треугольниками.
Определение равнобедренного треугольника
В равнобедренном треугольнике угол при основании - это угол, образованный двумя равными сторонами, а также линией, соединяющей середины этих сторон.
Угол при основании обычно обозначается буквой "b" или "B". Он всегда меньше других двух углов треугольника, так как равные стороны треугольника прилегают к нему.
| Стороны треугольника | Углы треугольника |
|---|---|
| Две стороны равны | Угол при основании |
| Одна сторона отличается от остальных | Два других угла |
Равнобедренные треугольники встречаются в различных областях математики и геометрии, а также в практических приложениях, таких как архитектура, инженерное дело и графика.
Свойства равнобедренного треугольника
У равнобедренного треугольника есть несколько свойств:
- Биссектриса угла при основании делит основание на две равные части.
- Медианы, проведенные к основанию, равны и пересекаются в точке, делящей каждую медиану пополам.
- Угол при основании равен полусумме двух других углов.
- Окружность, описанная около равнобедренного треугольника, проходит через середину основания и вершину треугольника.
Биссектриса – это линия, которая делит угол на две равные части. В равнобедренном треугольнике биссектриса угла при основании является высотой и медианой треугольника. Таким образом, биссектриса делит основание на две равные части.
Медиана – это линия, которая соединяет вершину треугольника с серединой противоположной стороны. В равнобедренном треугольнике медианы, проведенные к основанию (основание – сторона, не равная боковой стороне), равны и пересекаются в точке, которая делит каждую медиану пополам.
В равнобедренном треугольнике угол при основании равен полусумме двух других углов, то есть углу при боковой стороне и углу напротив боковой стороны.
Описанная окружность – это окружность, проходящая через все вершины треугольника. В равнобедренном треугольнике описанная окружность проходит через середину основания и вершину треугольника.
Поэтому равнобедренные треугольники обладают рядом интересных и полезных свойств, которые можно использовать при решении геометрических задач.
Как найти угол при основании
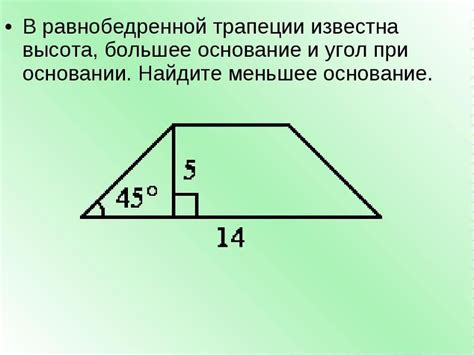
- Зная длины сторон треугольника, можно воспользоваться теоремой косинусов. Данная теорема состоит в следующем: квадрат длины биссектрисы равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.
- Если треугольник задан вершинами в пространстве, то можно воспользоваться методом векторного произведения двух векторов. Из полученного вектора можно найти его модуль, равный площади параллелограмма со сторонами, равными векторам, и зная модули векторов, можно найти синус угла между ними.
- Еще одним способом нахождения угла при основании является построение перпендикуляра из вершины треугольника на основание. В получившемся прямоугольном треугольнике можно найти основание и высоту. Зная эти данные, можно найти синус угла.
Используя данные методы, можно точно определить угол при основании равнобедренного треугольника.
Применение угла при основании равнобедренного треугольника

Один из основных примеров применения угла при основании равнобедренного треугольника – это в решении задач, связанных с построением и прямыми углами. Например, для построения перпендикуляра к прямой можно использовать свойство равнобедренного треугольника. Зная длину основания и угол при основании, можно точно определить длину перпендикуляра.
Также угол при основании равнобедренного треугольника используется в тригонометрии для вычисления значений тригонометрических функций. Например, зная длину основания и угол при основании, можно вычислить значения синуса, косинуса и тангенса этого угла. Такие вычисления широко применяются в физике, инженерии и других науках, где знание тригонометрии играет важную роль.
Угол при основании равнобедренного треугольника также встречается в архитектуре и дизайне. Благодаря своей симметрии и геометрическим пропорциям, равнобедренные треугольники используются в создании эстетически приятных и гармоничных форм и фигур. Они используются в дизайне зданий, логотипов, элементов интерьера и многих других аспектах дизайна и искусства.
Угол при основании равнобедренного треугольника – это не просто элемент геометрии, но и важный инструмент для решения задач в разных областях. Он находит применение в математике, физике, инженерии, дизайне и других науках и искусствах. Знание и использование свойств равнобедренного треугольника помогает решать разнообразные задачи, а также создавать эстетически приятные формы и композиции.



