Равнобедренные треугольники - это особый вид треугольников, которые имеют две равные стороны. В каждом равнобедренном треугольнике есть угол, называемый углом при основании. Что такое угол при основании и как его можно найти?
Основание равнобедренного треугольника - это сторона, которая не является равной другим сторонам. Угол при основании находится между основанием и одной из равных сторон. Обычно этот угол обозначается буквой "А".
Угол при основании равнобедренного треугольника всегда является углом, опирающимся на основание. Он также представляет собой угол между биссектрисой равнобедренного треугольника и основанием. Биссектриса - это линия, разделяющая угол на две равные части.
Как найти угол при основании? Если известны две равные стороны равнобедренного треугольника и угол между ними, то можно использовать теорему синусов или косинусов, чтобы найти угол при основании. Например, если известны длины двух равных сторон и угол между ними, то можно использовать теорему косинусов для вычисления значения угла при основании.
Угол при основании равнобедренного треугольника: определение и свойства
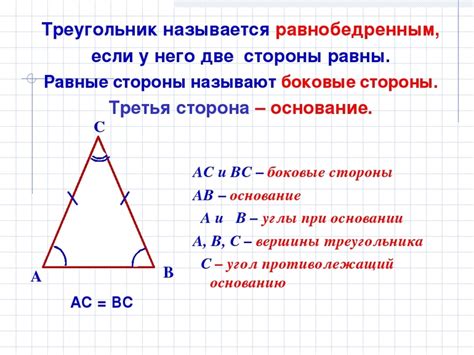
Данное определение говорит о том, что в равнобедренном треугольнике две стороны, выходящие из вершины основания, равны между собой. Это означает, что углы при этих сторонах также равны.
Свойства угла при основании равнобедренного треугольника:
- У равнобедренного треугольника углы при основании равны. Это означает, что если один угол при основании равнобедренного треугольника измеряет, например, 60 градусов, то другие углы при основании также будут иметь значение 60 градусов.
- Сумма углов при основании равна 180 градусов. Так как углы при основании равны, то их сумма будет равна сумме двух одинаковых значений, то есть 2x. Если обозначить один из углов при основании равнобедренного треугольника как x, то сумма будет: x + x = 2x. Известно также, что сумма углов треугольника равна 180 градусов, поэтому можно записать уравнение: 2x = 180, откуда следует, что x = 90. Таким образом, каждый из углов при основании равнобедренного треугольника равен 90 градусам.
Угол при основании равнобедренного треугольника является одним из важных понятий геометрии и находит применение при решении задач, связанных с данным типом треугольников. Знание его определения и свойств позволяет более полно осознать структуру равнобедренных треугольников и использовать его при решении задач различной сложности.
Угол при основании равнобедренного треугольника: определение
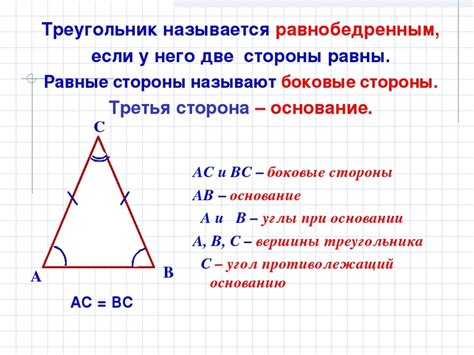
В равнобедренном треугольнике, у которого две стороны равны, угол при основании будет равен углу между этими сторонами. Иными словами, угол при основании равен половине значения угла между боковыми сторонами.
Угол при основании равнобедренного треугольника обычно обозначается символом α или β. Он может быть остроугольным, прямым или тупоугольным, в зависимости от величины угла между боковыми сторонами.
Свойства угла при основании равнобедренного треугольника
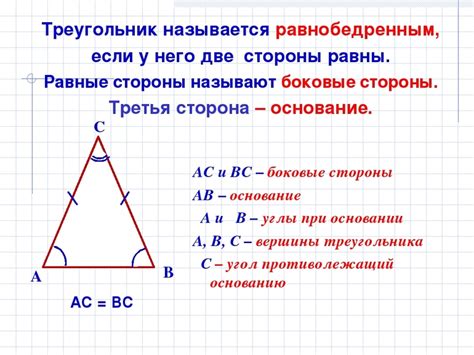
1. Угол при основании равнобедренного треугольника равен:
Для равнобедренного треугольника характерно, что основные углы (углы при основании) имеют одинаковую величину. Это свойство говорит о том, что угол при основании равнобедренного треугольника всегда является равным.
2. Угол при основании равнобедренного треугольника делит:
Угол при основании равнобедренного треугольника делит его вершину над основанием на две равные части. То есть, отрезок, соединяющий вершину треугольника с серединой основания, будет проходить через угол при основании и делить его пополам.
3. Угол при основании равнобедренного треугольника равен смежному углу:
Основные углы равнобедренного треугольника являются смежными. Это означает, что угол при основании равнобедренного треугольника равен углу, образованному боковой стороной и другой стороной треугольника.
4. Угол при основании равнобедренного треугольника – базовый угол:
Угол при основании равнобедренного треугольника считается базовым углом. Это связано с тем, что основание треугольника является самой длинной его стороной, а угол при основании – наибольшим углом внутри треугольника.
Знание свойств угла при основании равнобедренного треугольника позволяет выполнять геометрические вычисления и решать задачи, связанные с этим типом треугольников.



