В физике угол поворота радиуса окружности является одним из важных понятий, которое используется для измерения вращательных движений. Этот угол позволяет определить, насколько далеко или близко движется точка по окружности в процессе вращения.
Угол поворота радиуса окружности измеряется в радианах, градусах или любой другой единице угловой величины. Он обозначается символом "θ" и является мерой отклонения радиуса окружности от исходного положения до текущего положения.
Угол поворота радиуса окружности важен для понимания процесса вращения и определения угловых скоростей. Он также используется для расчета ряда физических величин, таких как угловое ускорение и угловой момент. Например, при анализе движения вращения твердого тела, угол поворота радиуса окружности позволяет определить энергию и момент импульса системы.
Определение угла поворота радиуса окружности
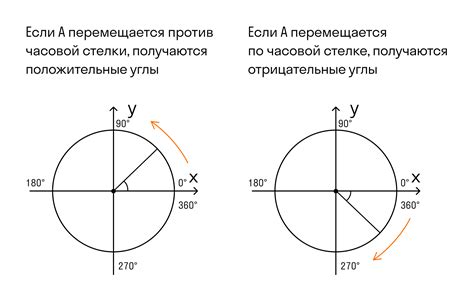
Угол поворота радиуса обычно измеряется в радианах и определяется как отношение длины дуги окружности, проходимой радиусом, к радиусу окружности:
Угол поворота радиуса = (длина дуги) / (радиус окружности)
Угол поворота радиуса также может быть выражен в градусах, где полный поворот окружности составляет 360 градусов.
Угол поворота радиуса играет важную роль в физике, особенно при изучении вращательного движения твердых тел. Он используется для определения угловой скорости и ускорения вращения, а также для прогнозирования траектории движения тел при вращении.
Понимание угла поворота радиуса окружности позволяет ученым и инженерам более точно оценивать и предсказывать движение вращающихся систем, что является необходимым при решении различных задач в физике, механике и инженерии.
Значение угла поворота в физике

Угол поворота определяет, насколько тело или точка перемещается по окружности или дуге. Он рассчитывается как отношение длины дуги, по которой перемещается тело, к радиусу окружности. Угол поворота может быть положительным или отрицательным, в зависимости от направления движения.
Значение угла поворота может быть использовано для определения изменения положения объекта в пространстве, а также для расчета скорости и ускорения объекта. Например, при расчете траектории движения частицы, угол поворота позволяет определить длину и направление перемещения. Это особенно важно при изучении кругового движения, такого как вращение электронов в атоме или движение планет вокруг Солнца.
Важно отметить, что угол поворота может быть измерен как в радианах, так и в градусах. В градусах полный угол поворота составляет 360°, а в радианах - 2π радианов.
Значение угла поворота лежит в основе многих физических законов и уравнений, и его понимание является необходимым для эффективного анализа и моделирования физических процессов.
Формула для вычисления угла поворота
Формула для вычисления угла поворота представляет собой отношение длины дуги окружности к радиусу:
θ = l / r
где:
- θ - угол поворота радиуса окружности;
- l - длина дуги окружности;
- r - радиус окружности.
Таким образом, для вычисления угла поворота необходимо знать длину дуги окружности и радиус соответствующего круга. Эта формула широко используется в физике, где изучаются движение и вращение тел.
Единицы измерения угла в физике
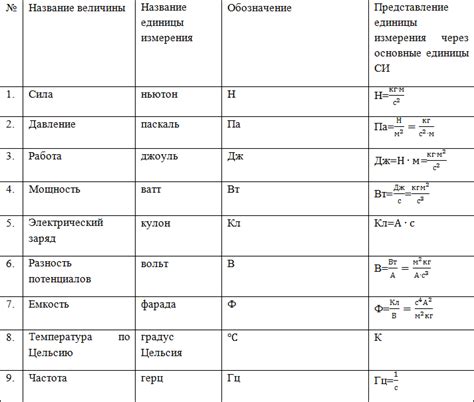
- Градус (°): это наиболее привычная и распространенная единица измерения угла. В одном круге содержится 360 градусов. Градус обозначается знаком ° и представляет собой 1/360 часть круга.
- Радиан (rad): это единица, которая используется в теории функций и анализе. В одном круге содержится приблизительно 6,28318 радианов. Радиан представляет собой угол, при котором длина дуги окружности равна радиусу.
- Гон (gon): это единица, которая используется в инженерии и геодезии. В одном круге содержится 400 гонов. Гон представляет собой 1/400 часть круга.
Для преобразования углов из одной единицы измерения в другую можно использовать следующие формулы:
- Для преобразования градусов в радианы: радиан = градус * (π / 180)
- Для преобразования радианов в градусы: градус = радиан * (180 / π)
- Для преобразования градусов в гоны: гон = градус * (10 / 9)
- Для преобразования гонов в градусы: градус = гон * (9 / 10)
Знание различных единиц измерения угла позволяет физикам и инженерам более гибко работать с угловыми величинами и проводить нужные расчеты.
Геометрическая интерпретация угла поворота
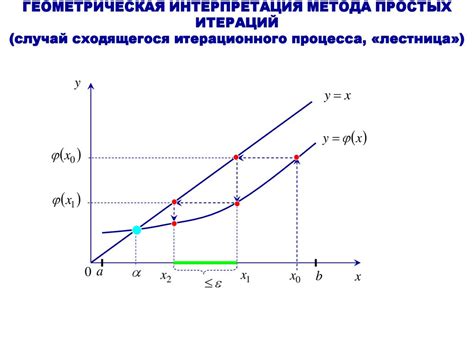
Угол поворота радиуса окружности в физике имеет также геометрическую интерпретацию. Для лучшего понимания этого понятия, необходимо представить себе окружность и ее радиус, а также точку, которая движется по окружности.
Если взглянуть на окружность с боковой стороны, то можно заметить, что радиус формирует определенный угол между начальным и конечным положением точки. Этот угол называется углом поворота или углом смещения.
Угол поворота указывает на разницу между начальным и конечным положением точки на окружности. Чем больше угол поворота, тем больше смещение точки. Если угол поворота равен 0, это означает, что точка вернулась в свое начальное положение.
Геометрическая интерпретация угла поворота позволяет связать его с длиной дуги окружности. Длина дуги можно выразить через круговую меру, равную 360 градусам или 2π радианам. Если у нас есть угол поворота α, то длина дуги обозначается как l = αr, где r - радиус окружности. Таким образом, угловое смещение и длина дуги пропорционально связаны друг с другом.
Геометрическая интерпретация угла поворота позволяет наглядно представить процесс движения точки по окружности и связать его с физическими законами, такими как закон сохранения углового момента или закон сохранения энергии. Знание угла поворота и его геометрической интерпретации позволяет более полно понять и анализировать различные физические явления и процессы, связанные с окружностями и их радиусами.
Кинематический аспект угла поворота
Угол поворота радиуса окружности определяется как отношение длины дуги, пройденной радиусом, к радиусу окружности. В случае движения по полной окружности, угол поворота равен 2π радианам или 360 градусам.
Кинематический аспект угла поворота позволяет определить скорость и ускорение тела во время движения по окружности. Вектор скорости всегда направлен касательно к окружности и перпендикулярен радиусу. Ускорение тела в данном случае направлено в сторону центра окружности и является радиусно-нормальным ускорением.
Угловая скорость определяется как отношение угла поворота за единицу времени и измеряется в радианах в секунду. Чем больше угловая скорость, тем быстрее происходит поворот радиуса окружности.
Угловое ускорение определяется как изменение угловой скорости за единицу времени и измеряется в радианах в секунду в квадрате. Оно характеризует изменение скорости поворота радиуса окружности и может быть постоянным или изменяющимся во время движения тела.
Понимание кинематического аспекта угла поворота позволяет анализировать и описывать движение тела по окружности, а также применять основные принципы физики в решении задач, связанных с этим типом движения.
Принцип сохранения угла поворота в физике

Для точного понимания принципа сохранения угла поворота, нам необходимо рассмотреть несколько ключевых понятий:
Радиус окружности: это расстояние от центра окружности до любой ее точки. Изменение радиуса приводит к изменению геометрических параметров окружности.
Скорость вращения: это физическая величина, отражающая изменение угла поворота в единицу времени. Изменение скорости вращения может привести к изменению кинематических характеристик вращения.
Принцип сохранения угла поворота утверждает, что при изменении радиуса окружности или скорости вращения, угол поворота остается постоянным. Это означает, что при изменении одного параметра (радиуса или скорости), другой параметр автоматически компенсируется таким образом, чтобы угол поворота оставался неизменным.
Принцип сохранения угла поворота находит широкое применение в физике, особенно при изучении движения тел в круговом или плоском вращении. С его помощью можно анализировать и предсказывать поведение систем, а также расчитывать значения физических величин на основе заданных параметров.



