Углы луча – это важный концепт в геометрии и физике. В простейшем понимании, угол луча представляет собой область пространства между двумя лучами, которые имеют общий начальный пункт, называемый вершиной. Углы луча можно встретить во множестве областей, включая физику, инженерию, архитектуру и многое другое.
Значение угла луча зависит от его величины. Угол может быть острый, прямой, тупой или полный. Острый угол имеет значение меньше 90 градусов, прямой угол равен 90 градусам, тупой угол больше 90 градусов, а полный угол равен 180 градусам.
Примеры использования углов луча тесно связаны с практическими применениями геометрии и физики. В архитектуре, например, углы луча играют важную роль в проектировании зданий и определении их пространственной организации. В физике, углы луча используются для описания направления и взаимного расположения объектов, особенно в оптике и аналогичных областях.
Что такое угол луча?
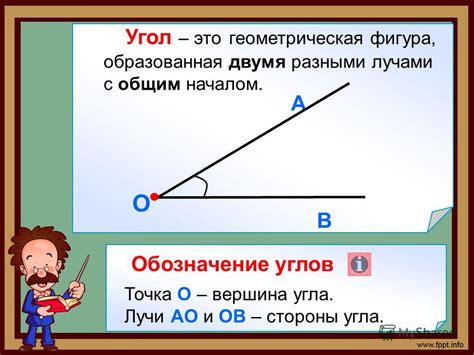
Угол луча измеряется в градусах или радианах. В школьной геометрии углы обычно измеряются в градусах. 1 градус равен 1/360 от полного оборота вокруг точки. В математике и физике могут также использоваться радианы – угловая мера, равная отношению длины дуги окружности к радиусу этой окружности.
Угол луча можно классифицировать в зависимости от его величины:
- Прямой угол – равен 90 градусам или π/2 радианам;
- Острый угол – меньше 90 градусов или π/2 радианов;
- Тупой угол – больше 90 градусов и меньше 180 градусов или π/2 радианов;
- Полный угол – равен 360 градусам или 2π радианам.
Углы могут применяться в различных областях науки и техники. Например, в физике угол луча используется при изучении отражения и преломления света, а в геодезии углы определяют направления между объектами на земной поверхности.
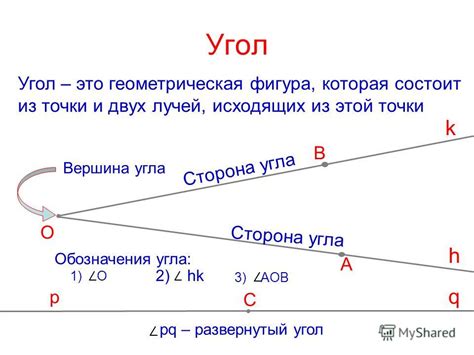
Значения угла луча
| Значение угла луча | Описание | Пример |
|---|---|---|
| 0° | Луч направлен вдоль оси X |  |
| 0° < угол < 90° | Луч направлен в I квадрант |  |
| 90° | Луч направлен вверх |  |
| 90° < угол < 180° | Луч направлен во II квадрант |  |
| 180° | Луч направлен вдоль оси Y |  |
| 180° < угол < 270° | Луч направлен в III квадрант |  |
| 270° | Луч направлен вниз |  |
| 270° < угол < 360° | Луч направлен в IV квадрант |  |
| 360° | Луч образует полный оборот |  |
Значения угла луча позволяют определить положение луча относительно начала координат и осей X и Y. Также это позволяет производить вычисления с углами и применять их в различных задачах и приложениях, включая геометрию, физику, компьютерную графику и многое другое.
Примеры использования угла луча
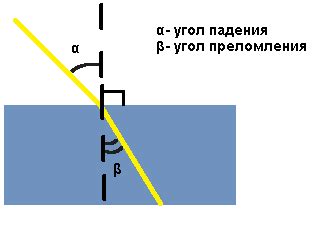
Геометрия: В геометрии угол луча используется для измерения отношения двух отрезков, образованных двумя лучами с общим началом. Он позволяет определить, насколько отклонены лучи от прямой линии или друг друга. Например, в треугольнике углы луча используются для определения типа треугольника (остроугольный, тупоугольный или прямоугольный) и его свойств (равносторонний, равнобедренный и т.д.). | Физика: В физике угол луча часто используется для описания направления движения света, звука и других электромагнитных волн. Например, при изучении оптики угол луча определяет угол падения, отражения и преломления света на границе раздела двух сред. |
Инженерия: В инженерии угол луча используется при проектировании и строительстве различных сооружений. Например, при проектировании мостов и зданий угол луча позволяет определить оптимальную форму и расположение элементов конструкции. | Геодезия: В геодезии угол луча используется для измерения направления и угла наклона земной поверхности. Например, при определении координат точек на местности или при построении карт и планов. |
Это только некоторые примеры использования угла луча. В общем, это важное понятие, которое находит свое применение в различных науках и областях жизни.
Знание угла луча позволяет выполнять различные вычисления и решать задачи в геометрии и физике. Например, в тригонометрии углы лучей используются для вычисления тригонометрических функций, таких как синус, косинус и тангенс. В оптике углы лучей определяют направление распространения света и позволяют рассчитывать отражение и преломление света на поверхностях.
Изучение углов лучей помогает развивать пространственное мышление, аналитические навыки и логическое мышление. Знание геометрии и углов лучей существенно полезно не только для учебы, но и во многих сферах нашей жизни, где требуется работа с пространственными объектами: архитектуре, строительстве, дизайне, механике и многих других.



