Прямоугольный треугольник - одна из самых известных и широко используемых геометрических фигур. Он имеет один прямой угол, который равен 90 градусам. Но помимо прямого угла, у прямоугольного треугольника есть еще два угла, которые могут быть различными.
Значения этих углов в градусах являются важными для различных расчетов и построений, связанных с прямоугольными треугольниками. Например, зная значения углов, можно найти длины сторон треугольника с помощью тригонометрических функций, таких как синус, косинус и тангенс.
Точные значения углов прямоугольного треугольника в градусах легко запомнить. Один из углов равен 90 градусам, второй угол равен 45 градусам, а третий угол также равен 45 градусам. Эти значения особенно удобны при решении задач, связанных с треугольниками, так как часто встречаются треугольники с углами 45 и 90 градусов.
Определение прямоугольного треугольника
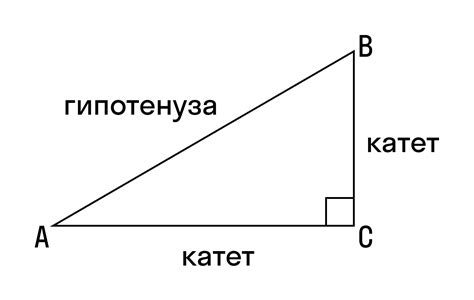
В прямоугольном треугольнике можно выделить особые свойства:
- Сумма всех углов прямоугольного треугольника равна 180 градусам. Поскольку один угол равен 90 градусам, то сумма двух оставшихся углов будет также равна 90 градусам.
- Стороны прямоугольного треугольника называются катетами и гипотенузой. Катеты - это две стороны, прилегающие к прямому углу, а гипотенуза - это сторона, противоположная прямому углу.
- В прямоугольном треугольнике длина гипотенузы всегда больше длины катетов. Это следует из теоремы Пифагора, которая гласит: квадрат длины гипотенузы равен сумме квадратов длин катетов.
Определение прямоугольного треугольника позволяет использовать его свойства для решения различных задач в геометрии и строительстве.
Основные свойства прямоугольного треугольника

| Свойство | Описание |
|---|---|
| Гипотенуза | Гипотенуза прямоугольного треугольника - это наибольшая из его сторон. Она расположена против прямого угла и является прямой границей между двумя катетами. |
| Катеты | Катеты прямоугольного треугольника - это две меньшие стороны, смежные с прямым углом. Они примыкают к гипотенузе и образуют ее стороны. |
| Углы | У прямоугольного треугольника всегда есть один прямой угол, равный 90 градусов. Другие два угла могут быть острыми (меньше 90 градусов) или тупыми (больше 90 градусов). |
| Теорема Пифагора | В прямоугольном треугольнике выполняется Теорема Пифагора, которая гласит: квадрат гипотенузы равен сумме квадратов катетов. Данная теорема является основой для решения множества задач и вычисления длин сторон треугольника. |
Знание основных свойств прямоугольного треугольника позволяет производить расчеты и проводить построения с использованием данных о его углах и сторонах.
Соотношение сторон в прямоугольном треугольнике
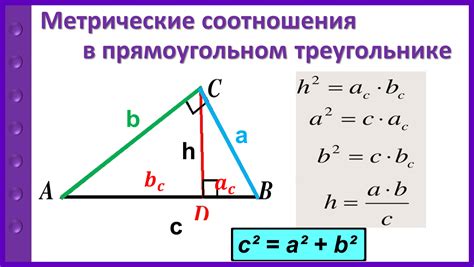
В прямоугольном треугольнике соотношения между его сторонами обладают определенными свойствами. Зная длину одной из сторон, можно найти длины остальных с помощью таких соотношений.
Основное соотношение сторон в прямоугольном треугольнике называется теоремой Пифагора: квадрат длины гипотенузы (самой длинной стороны) равен сумме квадратов длин катетов (двух меньших сторон).
Если гипотенуза прямоугольного треугольника равна c, а катеты равны a и b, то теорема Пифагора записывается следующим образом:
- a² + b² = c²
Это соотношение позволяет найти длины сторон прямоугольного треугольника, если известны длины других сторон.
Также в прямоугольном треугольнике существует соотношение сторон, называемое тангентом. Тангенс угла α определяется как отношение противоположного катета к прилежащему катету:
- tan(α) = a / b
Арктангенс принимает обратное значение и позволяет находить значения углов:
- α = arctan(a / b)
Таким образом, соотношение сторон в прямоугольном треугольнике позволяет нам определить длины и углы треугольника, что очень полезно при решении геометрических задач и построении фигур.
Формулы для расчета углов

1. Угол между гипотенузой (стороной противоположной прямому углу) и одним из катетов можно найти по следующей формуле:
α = arctan(a / b)
где α - угол противоположный катету a, b - другой катет.
2. Угол противолежащий гипотенузе находится с помощью тригонометрической функции синуса:
β = arcsin(b / c)
где β - угол противолежащий гипотенузе, c - гипотенуза.
3. Оставшийся угол треугольника можно найти по формуле:
γ = 90° - α - β
где γ - оставшийся угол треугольника, α и β - известные углы.
Эти формулы позволяют точно определить значения углов прямоугольного треугольника, что необходимо при выполнении различных расчетов и построений.
Практическое применение углов прямоугольного треугольника

Углы прямоугольного треугольника имеют широкое практическое применение в различных областях, включая геометрию, физику, инженерию, архитектуру и другие.
Один из наиболее известных способов использования углов прямоугольного треугольника - это использование их для расчетов и построений. Например, при строительстве зданий и сооружений нередко возникает необходимость определить углы для правильного размещения стен и других конструкций. Другой пример - в геодезии, углы прямоугольного треугольника используются для измерения расстояний и определения координат точек на земной поверхности.
Также углы прямоугольного треугольника используются в физике для решения задач, связанных с движением тела или силами, действующими на объекты. Например, при расчете траекторий бросания или полета объектов необходимо знать углы между векторами скорости и силой тяжести.
В архитектуре и дизайне углы прямоугольного треугольника используются для создания симметричных и гармоничных форм и пропорций. Например, золотое сечение, которое основывается на пропорциях прямоугольного треугольника, широко применяется в архитектуре и искусстве.
Инженеры и технические специалисты также используют углы прямоугольного треугольника для проведения работ, связанных с измерением и конструкцией. Например, при проектировании дорог и инфраструктуры необходимо учитывать углы поворотов и поворотные радиусы, чтобы обеспечить безопасность и комфорт движения.
Таким образом, углы прямоугольного треугольника играют важную роль в различных областях и находят применение в решении разнообразных задач, где требуется точное определение углов и их влияние на объекты и процессы.
Построение прямоугольного треугольника по заданным углам и сторонам
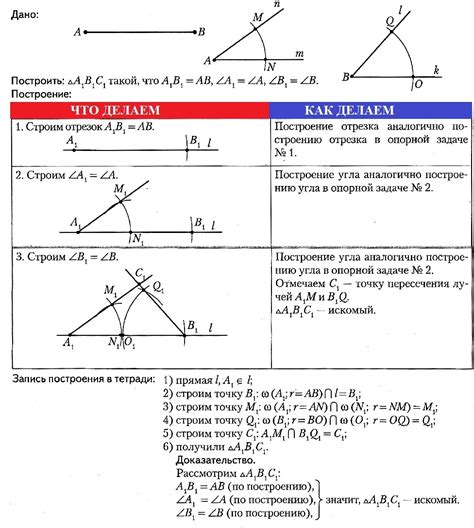
Для построения прямоугольного треугольника по заданным углам и сторонам требуется знание его углов и длин сторон. При этом, мы предполагаем, что углы заданы в градусах.
Поскольку мы знаем все углы треугольника, мы можем легко найти третий угол, исходя из того, что сумма всех углов треугольника равна 180 градусам.
Затем мы можем использовать теорему синусов, чтобы найти длины всех сторон треугольника. Теорема синусов утверждает, что отношение длины стороны к синусу её противолежащего угла равно постоянной величине для всех сторон треугольника. Это даёт нам возможность найти длины сторон, исходя из соответствующих углов.
После того, как мы найдем длины сторон, мы можем использовать их для построения треугольника на плоскости. Начиная с одной из вершин треугольника, мы строим отрезки равные найденным длинам. Затем соединяем концы этих отрезков, чтобы получить требуемый треугольник.
Построение прямоугольного треугольника по заданным углам и сторонам является важной задачей в геометрии и находит применение в различных отраслях науки и техники.
Примеры задач с прямоугольными треугольниками

Далее приведены несколько примеров задач, связанных с прямоугольными треугольниками:
Пример 1: Найти гипотенузу треугольника, если известны длины его катетов: a = 3 см, b = 4 см.
Решение: Воспользуемся теоремой Пифагора: гипотенуза в квадрате равна сумме квадратов катетов. То есть c^2 = a^2 + b^2.
Подставляя известные значения, получаем: c^2 = 3^2 + 4^2 = 9 + 16 = 25. Отсюда c = √25 = 5 см.
Ответ: Гипотенуза треугольника равна 5 см.
Пример 2: Дан треугольник с гипотенузой длиной 10 см и одним катетом длиной 6 см. Найти длину второго катета.
Решение: Снова воспользуемся теоремой Пифагора: c^2 = a^2 + b^2.
Подставляя известные значения и заменяя a и b на известные длины, получаем: 10^2 = 6^2 + b^2. Разрешаем уравнение относительно b: b^2 = 10^2 - 6^2 = 100 - 36 = 64, откуда b = √64 = 8 см.
Ответ: Второй катет треугольника равен 8 см.
Пример 3: Известно, что один из углов прямоугольного треугольника равен 45°. Найти значения остальных углов.
Решение: Сумма углов треугольника равна 180°. Так как один угол равен 90°, то сумма двух оставшихся углов будет равна 180° - 90° = 90°.
Поскольку два из трех углов треугольника уже известны (90° и 45°), то третий угол можно найти как разность суммы всех углов и суммы двух уже известных углов: 180° - 90° - 45° = 45°.
Ответ: Значения всех углов прямоугольного треугольника равны: 90°, 45° и 45°.



