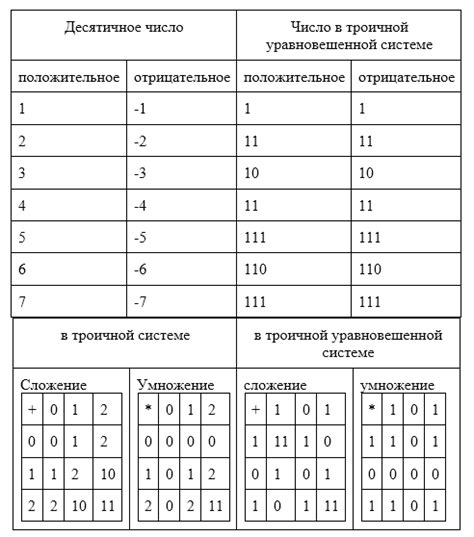
Троичная система счисления – это математический метод представления чисел, в котором используются три цифры: 0, 1 и 2. В отличие от десятичной системы, где используются десять цифр, троичная система позволяет представлять числа с использованием меньшего количества цифр.
Особенностью троичной системы является то, что она основана на степенях числа 3. В ней каждая позиция числа обозначает степень тройки. Например, число 10 в троичной системе будет означать 3 в степени 1, умноженное на 1, и 3 в степени 0, умноженное на 0.
Троичная система счисления используется в различных областях, например, в информатике. Она может быть полезной при работе с цифровыми сигналами, так как позволяет представлять состояния сигналов более эффективно. Также троичная система может использоваться в шифровании и безопасности данных, обеспечивая дополнительную сложность для взлома.
Преимущества троичной системы счисления
Троичная система счисления предлагает ряд преимуществ по сравнению с более популярными десятичной и двоичной системами. Вот некоторые из них:
- Экономия пространства и ресурсов: В троичной системе для представления чисел требуется меньше цифр, чем в десятичной или двоичной системах. Это позволяет сократить объем памяти, занимаемый числами, и сэкономить ресурсы, такие как электричество и время, затрачиваемое на обработку данных.
- Более компактное представление чисел: В троичной системе число может быть представлено с помощью меньшего количества цифр, что удобно при записи чисел на бумаге или в других носителях информации.
- Удобство при работе с триплетами: Троичная система позволяет представлять числа в виде триплетов, что существенно упрощает их сравнение и арифметические операции.
- Использование в криптографии: Троичные числа могут быть использованы для создания более безопасных алгоритмов шифрования, так как третье состояние (не только 0 и 1, но и 2) позволяет обеспечить дополнительную степень защиты данных.
- Разнообразные применения: Троичная система счисления может быть использована в различных областях, включая математику, информатику, физику, экономику и другие науки.
В целом, троичная система счисления представляет собой интересную альтернативу для более привычных десятичной и двоичной систем. Ее особенности позволяют эффективнее использовать ресурсы, упрощать операции с числами и применять в различных областях науки и технологий.
Троичные алгоритмы в криптографии

Троичная система счисления широко применяется в криптографии для решения различных задач безопасности и обеспечения конфиденциальности данных. Троичные алгоритмы используют трёхзначные символы (0, 1, 2) для представления информации, что позволяет эффективно шифровать и дешифровать данные.
Одно из наиболее распространенных применений троичных алгоритмов в криптографии - это создание хеш-функций, которые используются для обеспечения целостности и аутентичности данных. Хеш-функция преобразует входные данные произвольной длины в фиксированный троичный хеш-код, который выступает в качестве уникального идентификатора для этих данных. Такой подход позволяет эффективно проверять целостность файла или сообщения путем сравнения хеш-кода до и после передачи или хранения данных.
Троичные алгоритмы также используются для шифрования данных, что позволяет обеспечить их конфиденциальность. Одна из распространенных техник шифрования - троичное представление ключа, где каждый символ ключа заменяется на соответствующую троичную последовательность. После этого данные подвергаются троичному XOR-шифрованию с использованием этого ключа. Полученные зашифрованные данные могут быть безопасно переданы или хранены, поскольку без знания троичного ключа и алгоритма дешифрования их невозможно прочитать.
Троичные алгоритмы также находят применение в решении задач идентификации и аутентификации. Например, троичные коды могут использоваться для создания уникальных идентификаторов устройств или пользователей, а троичные алгоритмы могут использоваться для проверки подлинности этих идентификаторов.
Таким образом, троичные алгоритмы играют важную роль в криптографии, обеспечивая конфиденциальность, целостность и аутентичность данных. Использование троичной системы счисления позволяет эффективно решать задачи безопасности и защиты данных в различных областях, связанных с криптографией.
Использование троичных чисел в компьютерных операциях

В компьютерных операциях троичная система счисления может использоваться для решения определенных задач, где требуется более компактное представление данных или более эффективные операции.
Одной из областей применения троичных чисел является компрессия данных. В некоторых случаях использование троичной системы счисления позволяет сократить объем данных, что помогает уменьшить занимаемое пространство на диске и ускорить обработку информации.
Еще одним применением троичных чисел является криптография. В некоторых криптографических алгоритмах троичное представление данных может использоваться для зашифровки и расшифровки информации, обеспечивая дополнительную степень защиты.
Кроме того, троичные числа могут применяться в оптимизации алгоритмов и решении определенных вычислительных задач. Например, в некоторых алгоритмах троичные числа могут быть использованы для более эффективных и быстрых операций умножения или деления.
Однако следует отметить, что в обычных компьютерных системах троичная система счисления не широко использовалась из-за сложности ее реализации и ограниченности вариантов представления чисел. Вместо этого наиболее распространенными являются двоичная и десятичная системы счисления.
Тем не менее, в некоторых специализированных областях применение троичных чисел может быть полезным, позволяя эффективно решать определенные задачи и улучшать производительность систем.
Примеры применения троичной системы в реальной жизни
Троичная система счисления, основанная на знаках «0», «1» и «2», находит применение в различных областях человеческой деятельности. Вот несколько примеров использования троичной системы в реальной жизни:
1. Кодирование информации: В некоторых системах связи и хранения данных используют троичное представление для кодирования информации. Например, в оптических системах связи троичный код может быть использован для передачи информации на оптический сигнал.
2. Троичное программирование: В программировании троичная система может использоваться для разработки и оптимизации алгоритмов. Некоторые задачи, такие как поиск оптимального пути или задачи комбинаторной оптимизации, могут быть сформулированы и решены в троичном представлении.
3. Логические схемы: Троичная логика может быть применена в разработке логических схем. В отличие от двоичной логики, троичная логика имеет три возможных состояния: логическое «0», логическое «1» и логическую «неопределенность». Троичная логика может быть полезна при проектировании схем с большим количеством переменных.
4. Анализ данных: В некоторых областях анализа данных, таких как генетика и биоинформатика, троичное представление может использоваться для кодирования различных факторов, таких как генетические варианты, их влияния и связи.
Все эти примеры демонстрируют практическую ценность троичной системы счисления и подтверждают ее применимость в различных областях жизни. Оптимизация алгоритмов, эффективная передача информации и анализ данных - это только некоторые из возможностей применения троичной системы.
Различные способы представления троичных чисел

Существует несколько способов представления троичных чисел:
- Унарное представление
- Табличное представление
- Двоичное представление
Унарное представление - это самый простой способ представления троичных чисел, основанный на повторении символа для каждой единицы. Например, число 2 можно представить как "11" в унарном представлении.
Табличное представление - это представление троичных чисел в виде таблицы, где каждая цифра отображается в отдельной ячейке. Например, число 12 можно представить как:
| 1 | 2 |
Двоичное представление - это представление троичных чисел в виде двоичных чисел. Каждая цифра троичного числа заменяется на соответствующее двоичное значение. Например, число 201 можно представить в двоичной системе как "11001001".
Выбор способа представления троичных чисел зависит от конкретной задачи и требуемой точности представления. Каждый из предложенных способов имеет свои достоинства и недостатки, поэтому важно выбирать наиболее подходящий в каждой конкретной ситуации.
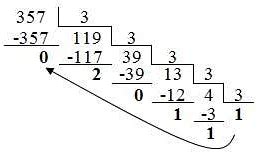
Перевод троичных чисел в другие системы счисления

Для перевода троичного числа в двоичную систему счисления необходимо разбить число на цифры, умножить каждую цифру на соответствующую степень числа 2 и сложить полученные произведения. Например, троичное число 210 переводится в двоичное следующим образом:
2 * 2^2 + 1 * 2^1 + 0 * 2^0 = 8 + 2 + 0 = 10 (в двоичной системе)
Для перевода троичного числа в десятичную систему счисления также необходимо разложить число на цифры, умножить каждую цифру на соответствующую степень числа 3 и сложить полученные произведения. Например, троичное число 210 переводится в десятичное следующим образом:
2 * 3^2 + 1 * 3^1 + 0 * 3^0 = 18 + 3 + 0 = 21 (в десятичной системе)
Таким образом, перевод троичных чисел в другие системы счисления осуществляется путем разложения числа на цифры, умножения каждой цифры на соответствующую степень основания системы счисления и сложения полученных произведений.
История троичной системы счисления

Троичная система счисления имеет довольно длинную и интересную историю. Она была известна в различных культурах и на протяжении многих веков использовалась для различных целей.
Первые упоминания о троичной системе счисления находятся в древних текстах, датируемых III веком до нашей эры. Однако, ее применение на практике не было широко распространено в те времена.
Одним из наиболее знаменитых примеров использования троичной системы счисления является Майя. Древние майя использовали троичные числа в своей астрономии и календаре. Они использовали три символа: точку, черту и нуль, чтобы представлять числа от 0 до 19, а также различные комбинации символов для больших чисел.
В других культурах троичная система счисления также была известна. Например, древние египтяне использовали троичные числа для конструирования пирамид и построения сложных ритуальных структур.
Сегодня троичная система счисления нашла свое применение в различных областях, таких как компьютерная техника и логика. Троичные вычисления могут быть более эффективными в некоторых случаях, например, в решении определенных логических задач и при программировании квантовых компьютеров.
История троичной системы счисления показывает, что она не только представляет интерес для математиков и исследователей, но также имеет практическое применение в различных областях науки и техники.



