Троичная система счисления – это система счисления, основанная на числе 3. В отличие от широко используемой десятичной системы, в которой используется 10 цифр (от 0 до 9), троичная система счисления состоит всего из трех цифр: 0, 1 и 2. Это означает, что любое число в троичной системе может быть представлено в виде комбинации этих трех цифр.
Применение троичной системы счисления может быть полезно во многих областях математики. Одной из основных областей, где она находит применение, являются вычисления с использованием логических элементов. В троичной системе можно представить все возможные комбинации значений для логических переменных true (истина) и false (ложь) – это очень полезно при решении логических задач и построении логических схем.
Кроме того, троичная система позволяет представить числа с большей точностью по сравнению с двоичной или десятичной системами. В троичной системе каждая позиция числа значительно влияет на его значение, что может быть полезно, например, при работе с очень большими или очень маленькими числами. Также троичная система может использоваться при решении некоторых математических задач, которые требуют более сложных вычислений.
Все это делает троичную систему счисления интересной и полезной для математиков и программистов. В качестве упражнения вы можете попробовать освоить троичную систему счисления, применить ее в своих вычислениях или решить математическую задачу, используя троичные числа. Это поможет расширить ваше понимание и навыки в области математики и компьютерных наук.
Основы троичной системы счисления

В троичной системе каждая позиция в числе имеет свое значение в зависимости от ее положения. Например, в числе 102 в троичной системе, число 2 находится в позиции единиц, число 0 в позиции троек и число 1 в позиции девяток.
Как и в десятичной системе, в троичной системе счисления также можно выполнять основные арифметические операции: сложение, вычитание, умножение и деление. Для этого используются аналогичные правила, но с учетом трех символов.
Троичная система счисления может быть использована в различных областях математики и информатики, например, при кодировании данных или в криптографии. Она может быть особенно полезна, когда нужно изобразить данные с большим количеством возможных состояний.
Определенные свойства троичной системы счисления делают ее уникальной и интересной для изучения. Например, при сложении двух чисел в троичной системе может возникнуть перенос больше, чем на одну позицию.
Как троичная система счисления отличается от десятичной
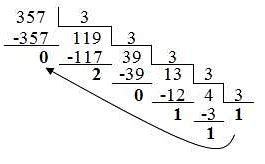
Троичная система счисления отличается от привычной нам десятичной системы счисления основными своими особенностями.
В троичной системе счисления существует всего три цифры: 0, 1 и 2. В десятичной системе счисления по аналогии используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
В десятичной системе счисления каждая позиция имеет вес, увеличивающийся в десять раз с каждым следующим разрядом. В троичной системе счисления вес каждой позиции увеличивается в три раза.
Также, в троичной системе счисления для обозначения чисел больше 2 необходимо использовать несколько цифр. Например, число 10 в троичной системе счисления соответствует числу 3 в десятичной системе.
Использование троичной системы счисления может быть полезным в некоторых областях математики, в особенности в теории информации и криптографии, где троичные операции и троичная логика могут быть эффективнее десятичных аналогов.
Преимущества и применение троичной системы счисления
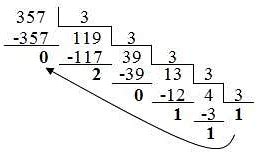
Троичная система счисления, основанная на использовании трех различных цифр (0, 1 и 2) вместо привычных двух (0 и 1), имеет несколько преимуществ и может быть полезна в различных областях математики и информатики.
- Компактность: Троичная система позволяет представлять числа с большей точностью в сравнении с двоичной системой. Например, число 7 в двоичной системе будет иметь вид 111, тогда как в троичной системе оно будет представлено всего двумя цифрами - 21.
- Упрощенная арифметика: В троичной системе счисления операции сложения, вычитания, умножения и деления проще выполнять, так как всего три разрешенных значения.
- Ошибка-обнаружение и коррекция: Троичная система более устойчива к ошибкам передачи данных по сравнению с двоичной системой. Благодаря наличию дополнительной цифры в троичной системе можно обнаружить ошибку при передаче или исправить ее.
Применение троичной системы счисления можно найти в различных областях, включая:
- Квантовые вычисления: Троичная система используется в некоторых моделях квантовых вычислений, где кьюбиты (квантовые биты) могут иметь три состояния - 0, 1 и 2.
- Цифровая логика: Троичные элементы могут использоваться в цифровых схемах и компьютерных архитектурах для улучшения эффективности и скорости вычислений.
- Кодирование и передача данных: Троичные коды могут использоваться для кодирования и передачи данных, особенно при работе с аналоговыми сигналами, такими как аудио и видео.
- Криптография: Троичные операции и алгоритмы могут использоваться в криптографических системах для защиты информации.
- Искусственный интеллект: В некоторых моделях искусственного интеллекта троичная система может быть использована для представления и обработки информации.
Троичная система счисления имеет свои особенности и преимущества, которые делают ее полезной и применимой в различных математических и информационных областях. Использование троичной системы может упростить выполнение арифметических операций, повысить точность представления чисел и повысить устойчивость передачи данных.
Применение троичной системы счисления в математике
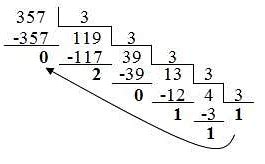
Троичная система счисления, основанная на числе 3, имеет свои применения в математике. Она может быть полезной при решении определенных задач и упрощении вычислений.
Одно из основных применений троичной системы счисления в математике - это использование ее в криптографии. В криптографических алгоритмах может быть необходимо представить числа в троичной форме для выполнения определенных операций. Это может обеспечить дополнительный уровень безопасности при шифровании данных.
Троичная система счисления также может быть полезной при вычислении делений и остатков. В некоторых случаях троичная система позволяет сократить количество операций и пространство для хранения данных. Например, при делении числа на 3, результатом может быть число, состоящее только из 0 и 1. Такие числа в троичной системе счисления могут быть представлены более компактно.
Еще одно применение троичной системы счисления связано с теорией информации. В теории информации каждый бит информации может быть представлен в виде символа 0, 1 или 2 в троичной системе. Это позволяет представлять информацию более эффективно и уменьшать объем передаваемых данных.
Троичная система счисления также может быть использована при решении математических головоломок и задач, основанных на логике. Некоторые задачи могут быть упрощены, если числа представлены в троичной системе.
Троичные числа в алгебре
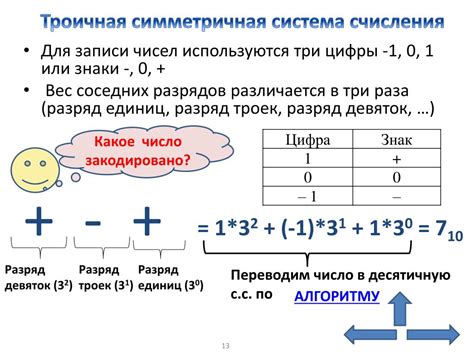
Троичная система счисления находит свое применение не только в информатике и электронике, но и в других областях, включая алгебру.
В алгебре троичные числа могут использоваться для представления различных объектов и свойств. Например, в линейной алгебре троичные числа можно использовать для задания коэффициентов при переменных в уравнениях и системах уравнений.
При работе с троичными числами в алгебре, также как и в десятичной системе, можно выполнять арифметические операции, такие как сложение, вычитание, умножение и деление. Каждая операция выполняется по определенным правилам, которые можно применять к троичным числам.
Кроме того, троичные числа могут быть использованы для представления логических значений в алгебре логики. Например, в логике троичные числа могут обозначать "истина", "ложь" и "неизвестно". Это позволяет более точно описывать логические выражения и вычислять их значения.
Таким образом, троичные числа в алгебре представляют собой полезный инструмент для работы с различными объектами и свойствами, а также для вычисления и представления данных.



