Тангенс – одна из основных тригонометрических функций, которая широко применяется в геометрии и физике. В частности, тангенс угла в прямоугольном треугольнике играет важную роль при решении различных задач, связанных с нахождением сторон и углов треугольника.
Тангенс угла может быть определен как отношение противолежащего катета к прилежащему катету прямоугольного треугольника. Иными словами, тангенс угла равен отношению длины противолежащего катета к длине прилежащего катета.
Формула для расчета тангенса угла в прямоугольном треугольнике выглядит следующим образом:
тангенс угла = противолежащий катет / прилежащий катет
Например, если мы имеем прямоугольный треугольник, у которого противолежащий катет равен 5, а прилежащий катет равен 3, мы можем рассчитать тангенс угла применяя формулу:
тангенс угла = 5 / 3
Определение тангенса угла
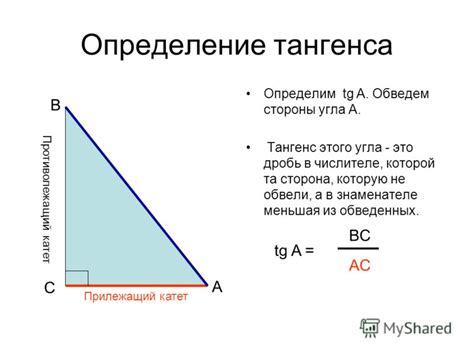
Тангенс угла А в треугольнике ABC можно выразить следующей формулой:
tg(A) = AB / BC
Где:
tg(A) – тангенс угла A;
AB – длина противолежащего катета;
BC – длина прилежащего катета.
Тангенс как отношение сторон прямоугольного треугольника
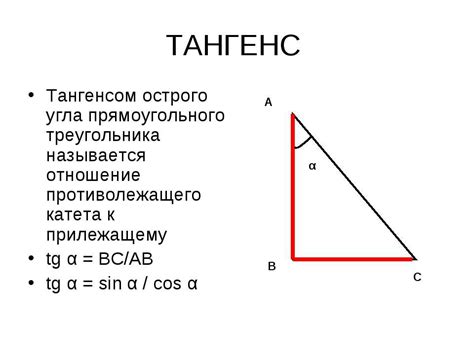
В прямоугольном треугольнике тангенс угла определяется как отношение длины противоположенного катета к длине прилежащего катета. Тангенс угла обозначается как tan(α) и рассчитывается по формуле:
tan(α) = AB/BC
Где AB - длина противоположенного катета, а BC - длина прилежащего катета.
Таким образом, тангенс угла позволяет определить, насколько круто или полого данный угол наклонен относительно оси X. Он является важным понятием в тригонометрии и находит широкое применение в геометрии, физике, инженерии и других науках.
Формула расчета тангенса угла
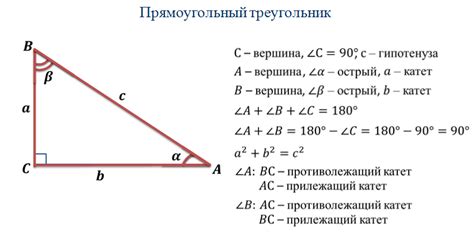
Тангенс угла в прямоугольном треугольнике можно определить с помощью формулы:
tg(α) = противолежащий катет / прилежащий катет
где α - угол, противолежащий катет которого мы исследуем.
Противолежащий катет – это отрезок, лежащий напротив угла α и стороны треугольника.
Прилежащий катет – это отрезок, примыкающий к углу α и стороне треугольника.
Таким образом, если известны значения противолежащего и прилежащего катетов, мы можем рассчитать тангенс угла α, используя указанную формулу.
Зависимость между тангенсом и противоположными и прилежащей сторонами
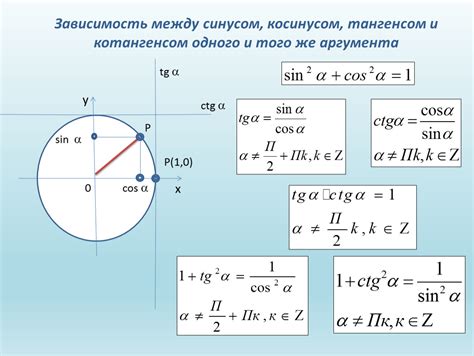
Тангенс угла в прямоугольном треугольнике определяется как отношение длины противоположной стороны к длине прилежащей стороны. Математически это может быть записано следующим образом:
тангенс угла = противоположная сторона / прилежащая сторона
Зная значения противоположной и прилежащей сторон, можно рассчитать тангенс угла. Обратно, зная значение тангенса и длину прилежащей стороны, можно найти длину противоположной стороны. Формула для расчета длины противоположной стороны при известном тангенсе и прилежащей стороне записывается так:
противоположная сторона = тангенс угла × прилежащая сторона
Тангенс угла позволяет связать длины сторон треугольника с углами и является важным инструментом в геометрии и тригонометрии. На практике, зная значения трех сторон треугольника, можно рассчитать все его углы, используя тангенс, синус и косинус.
Обратите внимание, что тангенс угла существует только для прямоугольных треугольников, где один из углов равен 90 градусов.
Применение тангенса угла
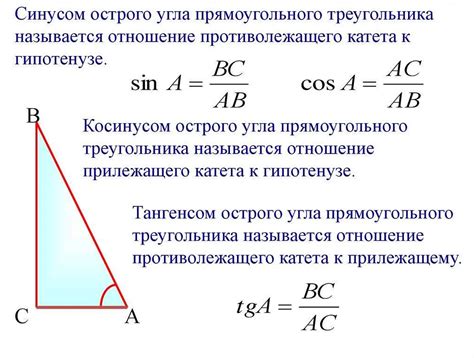
Одним из применений тангенса является нахождение значения угла. Если известны длины противолежащего и прилежащего катетов, можно использовать формулу тангенса, чтобы найти значение угла.
Также тангенс угла может использоваться для решения задач, связанных с высотой треугольника. Зная длину прилежащего катета и значение угла, можно найти длину высоты, опущенной на этот катет.
Помимо этого, тангенс угла может быть полезен в геодезии и навигации. Например, тангенс угла между горизонтом и линией взгляда используется для нахождения высоты наблюдаемого объекта.
Таким образом, знание тангенса угла позволяет решать разнообразные задачи, связанные с геометрией и тригонометрией, а также находить полезное применение в различных областях науки и практике.
Использование тангенса в геометрии и тригонометрии
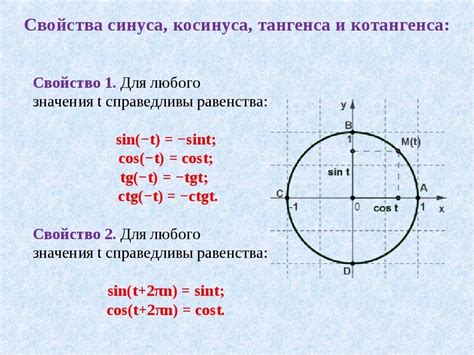
тангенс угла = противолежащий катет / прилежащий катет
Тангенс угла широко используется в геометрии и тригонометрии. Он помогает решать различные задачи, связанные с треугольниками и углами.
В геометрии тангенс применяют для определения высоты, расстояния и пропорций в прямоугольных треугольниках. С его помощью можно рассчитать углы и длины сторон треугольника, а также определить его площадь и периметр.
В тригонометрии тангенс - одна из шести тригонометрических функций, которая позволяет связать углы и стороны в произвольном треугольнике. Тангенс используется в формулах для решения треугольников разного типа и нахождения значений углов и сторон.
Знание свойств тангенса и умение его применять позволяет решать множество задач, связанных с геометрией и тригонометрией, а также находить практические применения в различных областях, таких как инженерия, физика, астрономия и др.
Свойства тангенса угла
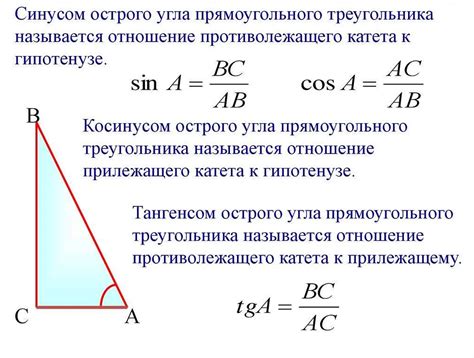
Тангенс угла обладает несколькими свойствами:
| Свойство | Формула |
|---|---|
| Периодичность | Если угол α имеет тангенс t, то угол α+π (или α+180°) имеет тангенс -t. |
| Отрезки на окружности | Тангенс угла α – это отношение длины отрезка, проведенного от начала декартовой системы координат до точки на единичной окружности с x-координатой cos α, до его y-координаты sin α. |
| Области значений | Значения тангенса угла лежат в интервале от -∞ до +∞. |
| Симметрия | Тангенс угла α и тангенс угла π-α, где α – произвольный угол, имеют одинаковое значение, если оно существует. |
Эти свойства тангенса угла являются важными при проведении различных геометрических и тригонометрических вычислений, а также при решении задач, связанных с углами в прямоугольных треугольниках.



