Тангенс - это тригонометрическая функция, определенная как отношение противолежащего катета к прилежащему катету прямоугольного треугольника. Зная значения противолежащего и прилежащего катетов, можно вычислить значение тангенса угла. В данной статье мы рассмотрим случай, когда тангенс равен 1/2 и определим соответствующий угол.
Для начала, стоит отметить, что отношение противолежащего катета к прилежащему катету можно записать в виде дроби. В нашем случае, тангенс равен 1/2, что означает, что противолежащий катет прямоугольного треугольника равен 1, а прилежащий катет равен 2.
Теперь, чтобы найти угол, который имеет такое значение тангенса, нам необходимо воспользоваться обратными тригонометрическими функциями. В случае с тангенсом, это функция арктангенс.
Что такое тангенс?
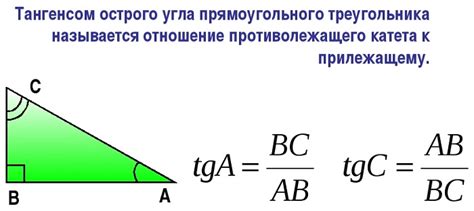
Тангенс можно обозначить как Tg или tg и вычислить по формуле:
Tg(угол 𝜃) = противолежащий катет / прилежащий катет
Значение тангенса может быть положительным, отрицательным или нулевым, в зависимости от значения угла 𝜃.
Тангенс обладает множеством математических свойств, которые используются в различных областях науки и техники. Он широко применяется в геометрии, физике, астрономии, инженерии и других дисциплинах.
Тангенс: связь синуса и косинуса
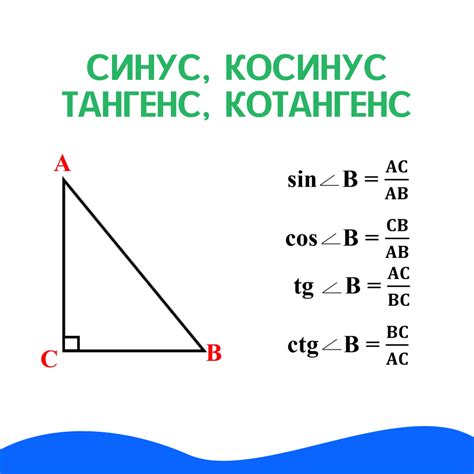
Тангенс угла относится к основным тригонометрическим функциям и выражает соотношение между значениями синуса и косинуса данного угла. Он определяется как отношение синуса угла к косинусу угла.
Формула для вычисления тангенса угла выглядит следующим образом:
tg(α) = sin(α) / cos(α)
Таким образом, если известны значения синуса и косинуса угла, то тангенс можно вычислить, разделив значение синуса на значение косинуса.
С помощью значений синуса и косинуса можно также вычислить тангенсное значение угла с помощью угловой точки на единичной окружности.
Более подробно информацию о тригонометрических функциях и их связи можно найти в соответствующих математических учебниках и онлайн ресурсах.
Как найти угол, который имеет тангенс равный 1/2?
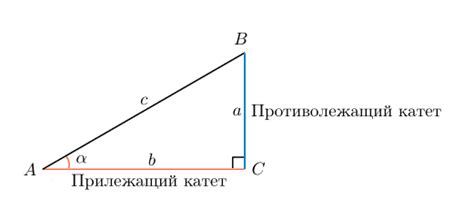
Тангенс угла определяется как отношение противоположной стороны к прилежащей стороне прямоугольного треугольника. Если известно значение тангенса и требуется найти соответствующий угол, следует использовать обратную функцию тангенса, которая называется арктангенс или тангенсальная функция. В нашем случае, тангенс равен 1/2, так что мы ищем угол, значение тангенса которого равно 1/2.
Для нахождения такого угла, мы должны использовать тангенсальную функцию, вычисляющую обратный тангенс (арктангенс). В математике это обозначается так: atan(1/2). Результатом вычисления будет угол, значение тангенса которого равно 1/2.
Использование калькулятора или математического программного обеспечения, можно найти приближенное значение этого угла, которое будет выражено в радианах или градусах. Например, если используется научный калькулятор, то необходимо нажать кнопку "atan" или "arctan", а затем ввести значение 1/2 и нажать кнопку "равно". Результат будет представлен в выбранной системе измерения углов.
Таким образом, чтобы найти угол, который имеет тангенс равный 1/2, необходимо использовать арктангенс, который позволит вычислить значение этого угла. Значение будет представлено в радианах или градусах и можно использовать для решения задач и проведения дальнейших вычислений.
Методы нахождения угла с заданным тангенсом
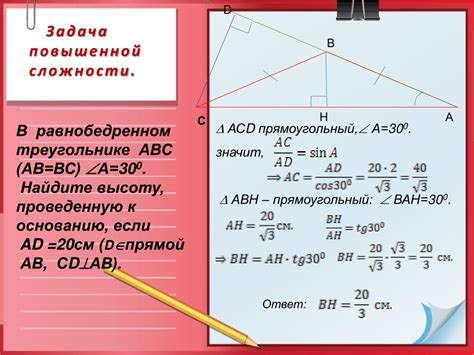
Нахождение угла с заданным тангенсом может быть полезным в различных математических и научных задачах. Существуют несколько методов для определения угла, который имеет определенное значение тангенса.
1. Таблицы тангенсов. Одним из самых простых способов найти угол с заданным тангенсом является использование таблиц тангенсов. В таблице можно найти значение тангенса и соответствующий ему угол. Однако этот метод не является точным и может быть неудобным при работе с большими значениями тангенса.
2. Калькуляторы и ПО для вычисления. Современные калькуляторы, программы и онлайн-ресурсы могут использовать алгоритмы и формулы для вычисления угла с заданным тангенсом. Они обеспечивают точные результаты и позволяют легко находить углы с любыми значениями тангенса.
3. Использование обратной тангенс функции. Обратная функция для тангенса называется арктангенс и обозначается как atan или tan-1. Её применение позволяет найти угол с заданным значением тангенса. Арктангенс может быть реализован в программном коде или использован в математических формулах.
4. Геометрические методы. В геометрии существуют специальные методы решения задач на нахождение угла с заданным тангенсом. Например, для прямоугольного треугольника со сторонами a и b, угол α можно найти по формуле α = arctan(b/a), если известны значения сторон треугольника.
Выбор метода нахождения угла с заданным тангенсом зависит от требуемой точности, доступных инструментов и контекста применения. В любом случае, знание различных методов и их использование может быть полезным для решения разнообразных задач.
Практическое применение угла с тангенсом 1/2

Угол, у которого тангенс равен 1/2, имеет особое значение в различных областях науки и техники. Такой угол называется половинным углом с тангенсом 1/2.
В геометрии половинный угол с тангенсом 1/2 является основой при решении задач, связанных с нахождением дополнительных углов, построением геометрических фигур и измерением наклонных поверхностей.
В физике половинные углы с тангенсом 1/2 применяются для определения направления векторов, угла падения и преломления света, а также для расчета силы и момента силы при взаимодействии тел.
В технике половинный угол с тангенсом 1/2 используется при проектировании угловых передач, калибровке инструментов с механическим механизмом и регулировке углов наклона в различных системах.
Знание основных свойств и применений углов с тангенсом 1/2 позволяет решать сложные задачи и справляться с ориентацией в пространстве на практике.
Примеры задач с решением

Найдите угол, тангенс которого равен 1/2.
- Решение находится в пределах одного периода тангенса, то есть от 0 до 360 градусов или от 0 до 2π радианов.
- Известно, что тангенс угла равен отношению противолежащего катета к прилежащему катету в прямоугольном треугольнике.
- По определению тангенса, 1/2 = противолежащий катет / прилежащий катет. Это может быть представлено как 1 / 2 = x / 1, где x - противолежащий катет и 1 - прилежащий катет.
- Решим уравнение: 1 / 2 = x / 1. Умножим оба числителя на 1 и оба знаменателя на 2, получим 2 = x.
- То есть, противолежащий катет равен 2.
- По теореме Пифагора, длина гипотенузы прямоугольного треугольника равна корню из суммы квадратов длин катетов.
- В данном случае, гипотенуза равна √(2^2 + 1^2) = √(4 + 1) = √5.
- Теперь, найдем синус и косинус угла. Синус равен противолежащему катету деленному на гипотенузу, а косинус - прилежащему катету деленному на гипотенузу.
- Синус угла равен 2 / √5 = (2√5) / 5.
- Косинус угла равен 1 / √5 = √5 / 5.
- Таким образом, угол, тангенс которого равен 1/2, имеет синус (2√5) / 5 и косинус √5 / 5.



