Треугольник – одна из основных геометрических фигур, которая пользуется популярностью в математике, физике, астрономии, а также других науках и прикладных областях. Он обладает множеством интересных свойств и возможностей, которые постоянно привлекают внимание исследователей и ученых.
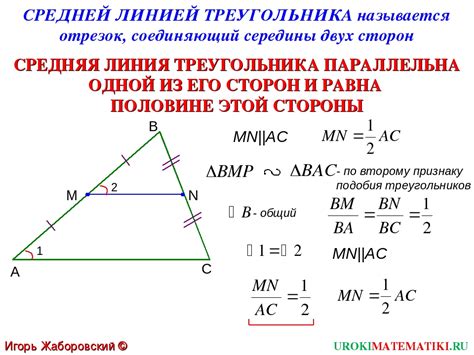
Одним из таких свойств является средняя линия треугольника. Слово «средняя» уже само по себе подразумевает, что эта линия делит другие линии или отрезки пополам или на равные части. В случае треугольника средняя линия делит противоположные стороны треугольника на две равные части и попадает в точку пересечения между вершиной треугольника и серединой противоположной стороны.
Средняя линия треугольника является одной из его интереснейших геометрических особенностей и находит многочисленное применение в различных областях. На основе этого свойства можно решить множество задач, касающихся треугольников и их особенностей. Благодаря средней линии можно определить центр масс треугольника, равномерно распределить его массу и многое другое.
Средняя линия треугольника ABC: определение и понятие
Средняя линия треугольника имеет несколько интересных свойств и применений. Вот некоторые из них:
- Средняя линия делит треугольник на два равных по площади треугольника.
- Средняя линия также является высотой треугольника, опущенной из его вершины.
- Средняя линия также является медианой треугольника, проходящей через вершину треугольника и середину противоположной стороны.
- Средняя линия является линией симметрии треугольника и делит его на две равные части.
Средняя линия треугольника ABC играет важную роль в различных геометрических теоремах и задачах. Например, с помощью средней линии можно доказать, что два треугольника являются подобными, а также находить центр тяжести и циркумцентр треугольника.
Условия и свойства средней линии

| Условие | Свойство |
|---|---|
| 1. Средняя линия параллельна третьей стороне | Средняя линия параллельна третьей стороне треугольника и равна половине её длины. |
| 2. Точка пересечения средних линий | Точка пересечения средних линий треугольника называется центром масс. Она равноудалена от вершин треугольника. |
| 3. Середины средних линий | Середины средних линий треугольника делят их в отношении 2:1. |
Используя эти условия и свойства средней линии, мы можем решать различные задачи и находить значения сторон и углов треугольника.
Как найти среднюю линию в треугольнике ABC
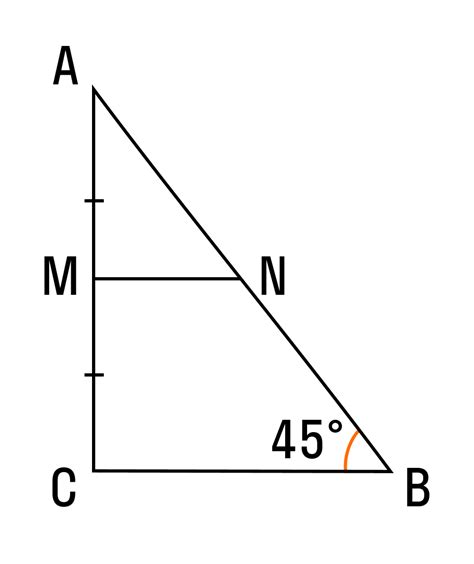
Для нахождения середины отрезка AB, необходимо найти среднее значение координат точек A и B. Если A(a₁, a₂) и B(b₁, b₂), то середина AB имеет координаты M((a₁ + b₁)/2, (a₂ + b₂)/2).
Аналогично, для нахождения середины отрезка BC, необходимо найти среднее значение координат точек B и C. Если B(b₁, b₂) и C(c₁, c₂), то середина BC имеет координаты N((b₁ + c₁)/2, (b₂ + c₂)/2).
Таким образом, мы получили две точки M и N, которые являются серединами сторон AB и BC соответственно. Чтобы найти среднюю линию DE, проведем прямую через эти точки.
| ABC | DE |
|---|---|
| AB | M |
| BC | N |
Средняя линия DE делит треугольник ABC на две равные по площади фигуры и проходит через точку D, которая является серединой стороны AC.
Средняя линия также является осью симметрии треугольника, то есть отражает все его точки относительно себя. Кроме того, средняя линия располагается на одной третьей отрезка, соединяющего вершину треугольника и середину противоположной стороны.
Использование средней линии треугольника ABC позволяет решать различные задачи, связанные с геометрией и треугольниками, например, находить площадь треугольника или находить координаты вершин треугольника по заданным координатам средних линий и длинам сторон.
Формулы для вычисления длины средней линии
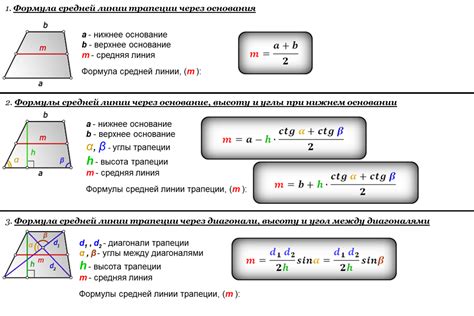
1. Если известны длины сторон треугольника (a, b и c), то длина средней линии (de) может быть вычислена по формуле:
de = (ab + ac + bc) / 2
2. Если известны координаты вершин треугольника (A(x1, y1), B(x2, y2) и C(x3, y3)), то длина средней линии (de) может быть вычислена по формуле:
de = sqrt(((x1 + x2 + x3) / 2)² + ((y1 + y2 + y3) / 2)²)
Где sqrt - это операция извлечения квадратного корня.
Независимо от используемой формулы, длина средней линии треугольника равна половине суммы длин двух сторон треугольника, через которые эта средняя линия проходит.
Вычисление длины средней линии может быть полезно при решении задач в геометрии, а также при определении геометрических свойств треугольника, таких как рассчет его площади или других характеристик.
Свойства и приложения средней линии треугольника ABC

Во-первых, средняя линия делит треугольник на два равных по площади треугольника. Это следует из того факта, что середины сторон делят их наполовину, и вершина треугольника типично лежит на средней линии.
Во-вторых, длина средней линии равна половине суммы длин двух других сторон треугольника. Это означает, что если известны длины двух сторон треугольника, можно легко найти длину средней линии по формуле: средняя линия = (сторона1 + сторона2) / 2.
Средняя линия также может использоваться для нахождения третьей стороны треугольника, если известны длины двух других сторон. Если известны сторона1 и сторона2, а средняя линия является третьей стороной треугольника, то длина средней линии равна разности длин двух других сторон: средняя линия = |сторона1 - сторона2|.
Помимо своих геометрических свойств, средняя линия также может быть использована в различных приложениях. Например, она может быть использована для построения треугольника по заданной стороне и его средней линии. Это может быть полезно при решении задач, связанных с конструированием и проектированием.
Таким образом, средняя линия треугольника ABC обладает не только геометрическими свойствами, но и имеет ряд практических приложений, что делает ее полезным инструментом при работе с треугольниками.
Свойства средней линии
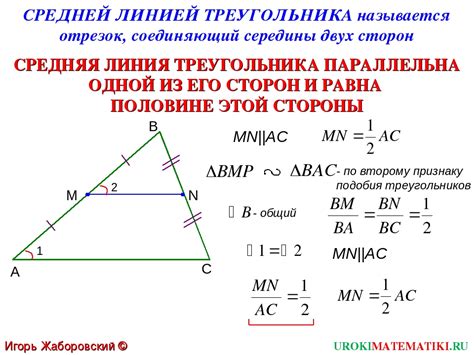
1. Длина средней линии равна половине длины соответствующей стороны треугольника.
Средняя линия, проведенная из вершины треугольника к середине противоположной стороны, всегда делит эту сторону на две равные части. Другими словами, длина средней линии равна половине длины соответствующей стороны треугольника.
2. Средние линии в треугольнике пересекаются в одной точке - центре тяжести треугольника.
Средние линии треугольника всегда пересекаются в одной точке - центре тяжести треугольника. Это означает, что точка пересечения средних линий является центром масс треугольника, в котором можно считать, что сосредоточена вся его масса.
3. Площадь треугольника, образованного средними линиями, равна четверти площади исходного треугольника.
Если в треугольнике провести средние линии, то они разделят треугольник на четыре меньших треугольника, каждый из которых будет иметь равную площадь. Площадь треугольника, образованного средними линиями, будет равна четверти площади исходного треугольника.
Таким образом, свойства средней линии в треугольнике являются важными для решения различных задач и нахождения различных параметров треугольника.
Применение средней линии в реальной жизни

Средняя линия треугольника ABC обладает множеством свойств, которые находят свое применение в различных областях реальной жизни. Рассмотрим некоторые из них:
| Свойство | Применение |
|---|---|
| Средняя линия равна половине основания | В строительстве, для определения равенства отрезков. Например, при замерах и расчетах длин стен. |
| Средняя линия делит треугольник на два равных по площади треугольника | В геодезии, для определения площадей участков земли. Например, при проектировании и разработке территории. |
| Средняя линия является осью симметрии треугольника | В дизайне и искусстве, для создания симметричных композиций. Например, при разработке логотипов и графических изображений. |
| Средняя линия проходит через центр масс треугольника | В физике, для расчета центра масс тела. Например, при исследовании баланса и равновесия объектов. |
Кроме указанных применений, средняя линия треугольника может быть использована в различных математических и инженерных расчетах, геометрическом моделировании и других областях науки и техники. Благодаря своим свойствам, средняя линия является важным инструментом в решении различных задач и проблем, связанных с треугольником ABC.



