Вершины и звенья ломаной линии – это основные понятия, используемые в геометрии для описания некоторых графических изображений. Ломаная линия является набором отрезков, соединяющих вершины, которые являются точками пересечения этих отрезков. Таким образом, вершины обозначают точки, в которых линия меняет свое направление или форму.
Звенья ломаной линии – это отрезки, составляющие линию и соединяющие вершины. Количество звеньев определяет количество отрезков в ломаной линии. Звенья могут быть прямыми или кривыми, в зависимости от формы ломаной линии и направления ее поворотов в вершинах.
Вершины и звенья ломаной линии играют важную роль при построении геометрических фигур и решении различных задач. Они позволяют определить форму, длину, углы и направление линии. Вершины и звенья также использованы в компьютерной графике и дизайне для создания кривых и декоративных элементов.
Таким образом, понимание вершин и звеньев ломаной линии позволяет лучше визуализировать и анализировать графические изображения, а также использовать их в различных областях, требующих работу с геометрическими фигурами и компьютерной графикой.
Вершины и звенья ломаной линии
Вершины являются основными элементами ломаной линии и определяют ее форму и направление. Каждая вершина имеет свои координаты, которые указывают ее положение на плоскости. Вершины могут быть произвольными точками или расположены на координатной сетке.
Звенья ломаной линии представляют собой отрезки, соединяющие две соседние вершины. Длина каждого звена может быть различной и зависит от конкретной ломаной линии. Звенья помогают определить форму и гладкость ломаной линии.
Ломаные линии могут иметь различное количество вершин и звеньев в зависимости от задачи или желаемого эффекта. Они широко применяются в геометрии, строительстве, компьютерной графике и дизайне для создания разнообразных фигур и изображений.
Вершины и звенья ломаной линии играют важную роль в ее визуальном представлении и определяют ее характеристики. Понимание этих элементов помогает лучше понять структуру и свойства ломаных линий.
Основные понятия ломаной линии
Звенья ломаной линии – это отрезки, которые соединяют вершины ломаной. Они являются составными частями ломаной линии и определяют ее форму и направление.
Количество вершин и звеньев в ломаной линии может быть различным. Ломаные линии могут иметь несколько вершин и звеньев или быть прямой линией, состоящей из двух вершин и одного звена.
Ломаные линии используются в различных областях: в геометрии, графике, картографии, компьютерной графике и дизайне. Они позволяют визуально представить сложные формы и упростить отображение графической информации.
Вершины и звенья ломаной линии являются важными элементами для анализа и изучения графических моделей, а также для создания эффектных визуальных композиций.
Значение вершин в ломаной линии
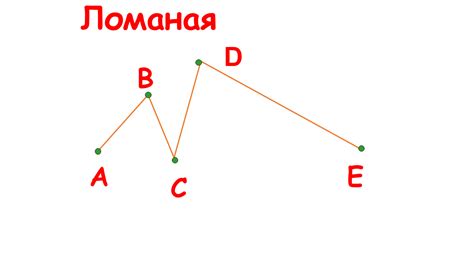
Значение вершин в ломаной линии заключается в определении направления изменения трассы фигуры. Вершины определяют, куда и каким образом будет изменяться направление ломаной линии.
Каждая вершина может иметь определенные свойства и характеристики, которые могут быть использованы для дальнейшей работы с ломаной линией. Например, вершины могут иметь координаты, которые определяют их положение в пространстве. Координаты вершин могут быть использованы для расчета длины каждого звена ломаной линии или для определения угла между звеньями.
Вершины также могут использоваться для определения поворотов или изгибов ломаной линии. Когда ломаная линия меняет свое направление на вершине, это может быть интерпретировано как поворот фигуры в этой точке. Угол поворота может быть определен с использованием координат вершин или других геометрических данных.
Таким образом, вершины в ломаной линии имеют важное значение для понимания и работы с данной геометрической фигурой. Они определяют направление изменений формы и могут быть использованы для расчетов и анализа различных характеристик ломаной линии.
Роль звеньев в ломаной линии
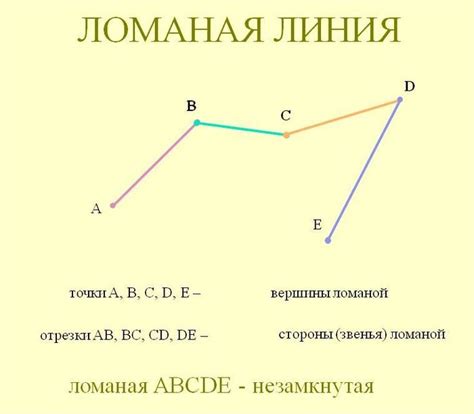
Каждое звено определяет направление движения линии и привязывает каждую вершину к ее соседним вершинам. Они позволяют определить точки, где ломаная меняет направление. Благодаря звеньям, ломаная линия может изгибаться и принимать различные формы.
Расстояние между звеньями может быть разным, что приводит к различной кривизне и длине каждого отрезка ломаной. Это делает звенья важными компонентами при создании геометрических фигур и моделей. Кроме того, звенья могут быть использованы для рассчета длины ломаной линии и определения ее геометрических свойств.
Важно помнить, что каждое звено является частью всей ломаной линии и влияет на ее общую форму. Если изменить положение или свойства одного звена, это может привести к изменению всей линии. Таким образом, звено является неотъемлемой частью ломаной линии и имеет непосредственное влияние на ее свойства и характеристики.
Геометрическое представление ломаной линии
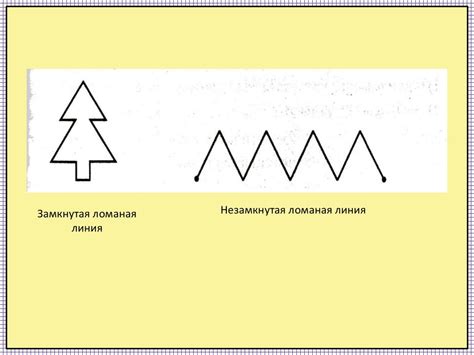
Для геометрического представления ломаной линии используются координаты вершин. Координаты – это числовые значения, определяющие положение точки на плоскости. В двумерном пространстве координатами точки обычно являются значения по оси X (горизонтальной оси) и оси Y (вертикальной оси).
Ломаная линия строится путем соединения вершин последовательно, при этом каждое звено представляет собой отрезок прямой линии. Таким образом, геометрически ломаная линия представляет собой совокупность отрезков, образующих криволинейное соединение точек на плоскости.
Геометрическое представление ломаной линии позволяет анализировать ее свойства и характеристики, такие как длина, углы между звеньями, направление и т.д. Это важно для различных областей знаний, включая геометрию, картографию, архитектуру, дизайн и другие.
Применение ломаных линий в графике
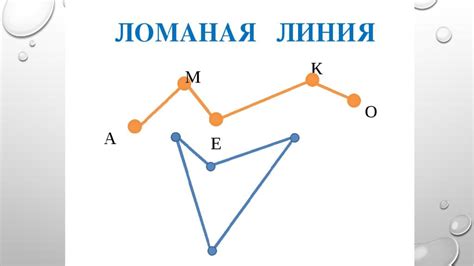
Одним из основных применений ломаных линий в графике является представление различных данных и информации. Например, ломаные линии могут использоваться для отображения временных рядов, изменения значений показателей, трендов и т.д. В таких случаях вершины ломаной линии представляют конкретные моменты времени или значения, а звенья – участки между этими моментами или значениями.
Ломаные линии также часто применяются для построения графиков функций. В этом случае вершины ломаной линии представляют значения функции в разных точках, а звенья – участки графика между этими точками. Такая представление графика функции позволяет визуально оценить ее поведение и свойства, такие как производные, максимумы и минимумы, сходимость и др.
Другим применением ломаных линий в графике является построение контуров и силуэтов объектов. В этом случае вершины ломаной линии отображают границы объекта, а звенья – его форму и структуру. Такое представление объектов позволяет удобно визуализировать их в пространстве, определить размеры, пропорции и др.
Таким образом, применение ломаных линий в графике широко разнообразно и зависит от конкретных задач и требований. Однако, в любом случае, ломаные линии являются мощным инструментом для визуализации данных, функций и объектов.
Математическое определение вершин и звеньев
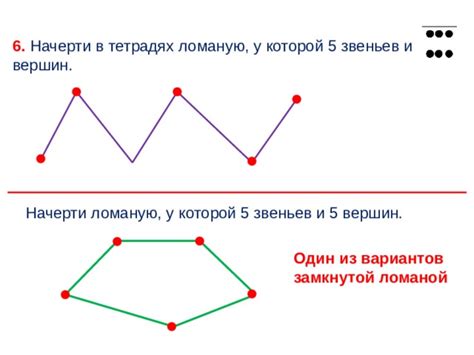
Вершина ломаной линии обладает определенными свойствами. Она имеет два смежных звена, которые соединяют ее с двумя соседними вершинами. Каждое звено соединяет две соседние вершины и имеет определенную длину. Чтобы определить положение вершин и звеньев в пространстве, могут использоваться координаты этих точек.
Математическое определение вершин и звеньев ломаной линии позволяет анализировать их характеристики и свойства. Например, можно изучать длины звеньев, углы между звеньями и другие параметры, используя методы математического анализа и геометрии. Это позволяет решать различные задачи, связанные с ломаными линиями, в том числе визуализацию, аппроксимацию и нахождение оптимальных путей в них.
Свойства вершин и звеньев ломаной линии
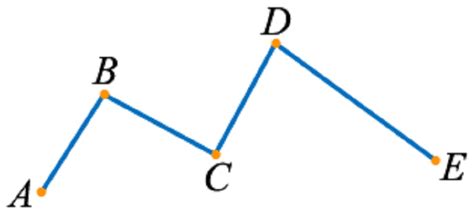
Свойства вершин:
- Координаты: каждая вершина определяется своими координатами на плоскости или в пространстве.
- Порядок: вершины нумеруются в последовательности, их порядок определяет форму линии.
- Углы: в точках соединения звеньев вершины могут образовывать углы, которые могут быть острыми, прямыми или тупыми.
- Точность: вершины могут быть заданы с различной точностью, в зависимости от реализации ломаной линии.
Свойства звеньев:
- Длина: каждое звено имеет свою длину, которая определяет масштаб фигуры.
- Направление: звенья могут быть выпуклыми или вогнутыми внутрь ломаной линии.
- Сглаживание: некоторые реализации ломаных линий позволяют сглаживать углы между звеньями для более плавного отображения.
- Толщина: звенья могут иметь различную толщину для визуального эффекта.
Знание свойств вершин и звеньев ломаной линии позволяет эффективно работать с такими фигурами и использовать их в различных задачах, включая графику, компьютерные игры и моделирование.



