Проекция гаусса – это математический метод, который позволяет представить многомерные данные в более удобной форме. Он основан на принципах гауссового распределения, которые широко используются в статистике и машинном обучении.
Основная задача проекции гаусса – снизить размерность данных, сохраняя при этом максимальное количество информации. Это позволяет упростить анализ и визуализацию данных, а также улучшить производительность алгоритмов обработки.
Процесс проекции гаусса включает в себя несколько этапов. Сначала данные преобразуются при помощи гауссовой функции, которая сглаживает их и устраняет шум. Затем применяются методы линейной алгебры, чтобы представить данные в новом пространстве с более низкой размерностью. Наконец, производится переход обратно к исходным данным, чтобы получить проекцию гаусса.
Проекция гаусса находит широкое применение в различных областях. В биоинформатике она используется для анализа и классификации геномных данных. В компьютерном зрении она помогает обрабатывать изображения и распознавать образы. В анализе текстов она может быть полезна при выявлении тематик и кластеризации документов.
Сущность проекции гаусса
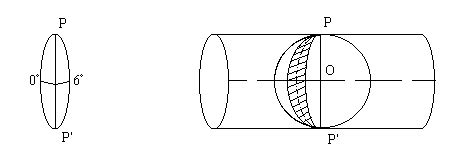
$$g(x) = A \cdot e^{-\frac{(x - \mu)^2}{2\sigma^2}}$$
где:
- A - амплитуда (максимальное значение функции);
- μ - среднее значение (центр функции);
- σ - стандартное отклонение (размер функции).
Проекция гаусса используется для аппроксимации различных типов данных, таких как изображения, звук, временные ряды и многие другие. Она обладает рядом преимуществ, включая гладкость аппроксимации и возможность регулировки амплитуды, среднего значения и стандартного отклонения функции для достижения наилучших результатов.
Применение проекции гаусса включает в себя такие области как обработка изображений, сжатие данных, предсказание временных рядов, распознавание образов и многие другие.
Принципы проекции гаусса
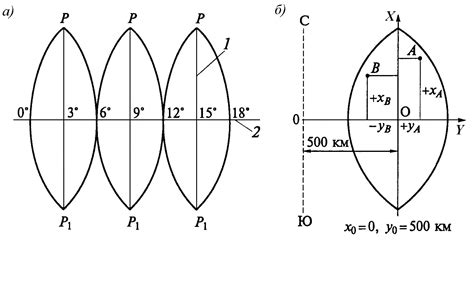
Главная идея проекции гаусса заключается в представлении данных в виде компактного набора параметров, обеспечивающих наилучшее приближение гауссовому распределению и минимальную потерю информации. Это позволяет существенно сократить размеры исходных данных без значительной потери качества и релевантной информации о них.
Основными принципами проекции гаусса являются:
- Уникальность: Каждый набор данных имеет свое уникальное представление в виде параметров гауссового распределения. Это обеспечивает сохранение исходной информации о данных при их сжатии.
- Независимость: Параметры гауссового распределения являются независимыми друг от друга, что упрощает анализ и обработку данных.
- Оптимальность: Проекция гаусса обеспечивает наилучшую аппроксимацию исходных данных с помощью параметров гауссового распределения, минимизируя потери информации.
Преимущества использования проекции гаусса включают высокую эффективность сжатия данных, сохранение технических и семантических характеристик исходных данных, а также возможность обратного восстановления и визуализации данных без значительной потери качества.
Применение проекции гаусса может быть найдено в различных областях, таких как сжатие изображений и видео, улучшение качества изображений, фильтрация шума, а также в генерация и анализ статистических данных.
Применение проекции гаусса
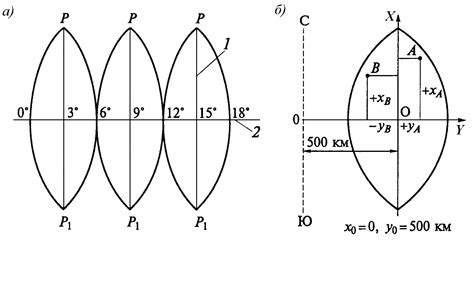
1. Обработка сигналов и изображений: Проекция гаусса активно используется для фильтрации и обработки сигналов различной природы, таких как аудио-сигналы и сигналы видео. Она позволяет значительно улучшить качество сигнала и удалить шумы, что особенно важно в таких областях, как медицинская диагностика и обработка изображений.
2. Классификация и распознавание: Проекция гаусса может быть использована для классификации и распознавания объектов и образов. Этот метод позволяет снизить размерность данных, сохраняя при этом наиболее информативные признаки. Он находит применение в различных областях, таких как компьютерное зрение, распознавание лиц и рукописного текста.
3. Машинное обучение и статистика: Проекция гаусса широко применяется в области машинного обучения и статистики. Она используется для уменьшения размерности данных и извлечения информации, что способствует более эффективному обучению моделей и повышает точность прогнозов. Проекция гаусса также может быть использована для снижения размерности больших данных, что помогает обрабатывать и анализировать информацию более эффективно.
4. Реконструкция и восстановление: Проекция гаусса может быть применена для восстановления и реконструкции данных, особенно в случаях, когда доступна только ограниченная информация. Она позволяет восстановить пропущенные или поврежденные данные, что имеет большое значение в областях, таких как передача и хранение информации, медицинская диагностика и астрономия.
Проекция гаусса продемонстрировала свою эффективность и применимость в различных областях науки и техники. Она является ценным инструментом для обработки данных, анализа образов и принятия решений на основе статистической информации.
Проекция гаусса: математическая модель
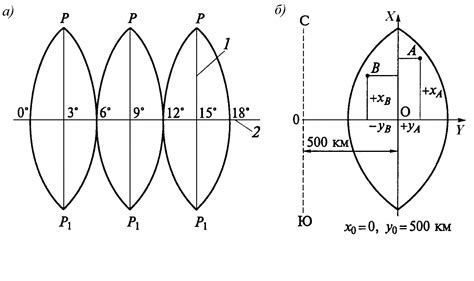
Гауссово распределение имеет следующий вид:
P(x) = (1 / (σ * √(2π))) * e^(-(x - μ)^2 / (2σ^2))где:
P(x) - вероятность нахождения значения x в данном распределении,σ - стандартное отклонение распределения,μ - математическое ожидание распределения.Проекция гаусса используется в различных областях, включая статистику, физику, экономику, машинное обучение и другие. Она позволяет описывать случайные величины с помощью гауссовой функции и анализировать их свойства.
Проекция гаусса широко применяется в статистическом анализе данных. Она помогает моделировать и предсказывать распределение случайных величин и использовать его для решения различных задач, таких как прогнозирование, классификация и кластеризация данных. Важной особенностью гауссовой проекции является то, что она позволяет описывать большинство естественных явлений, так как многие из них подчиняются гауссовому распределению.
В заключении, проекция гаусса представляет собой математическую модель, основанную на гауссовом распределении. Она позволяет описывать и анализировать случайные величины, а также широко используется в различных областях науки и техники.
Математические основы проекции гаусса

Гауссова функция, также известная как нормальное распределение или колоколообразное распределение, определяется математической формулой:
f(x) = A * exp(-(x - μ)² / (2σ²))
В этой формуле, x - значение независимой переменной, μ - среднее значение, σ - среднеквадратическое отклонение, A - амплитуда.
Проекция гаусса использует гауссовы функции для представления изображений или областей. Каждая функция представляет собой двумерное ядро, которое может быть размещено в определенной точке изображения. Объединение этих ядер дает приближенное представление оригинального изображения.
Проекция гаусса находит применение в различных областях, включая сжатие изображений, извлечение особых точек, распознавание образов и многие другие. Она позволяет представлять большие объемы данных компактным и информативным образом.
Важно отметить, что проекция гаусса - это приближенный метод и соответствие между исходным изображением и его проекцией не всегда точное.
Примеры применения математической модели

Математическая модель проекции гаусса находит свое применение в различных областях науки и техники. Ниже приведены некоторые примеры ее использования:
1. Обработка сигналов: Модель гауссовой проекции широко применяется в цифровой обработке сигналов для фильтрации, сглаживания и восстановления искаженных или зашумленных сигналов. Она позволяет более эффективно обрабатывать данные, учитывая их вероятностные свойства.
2. Обучение нейронных сетей: Модель гауссовой проекции используется в обучении нейронных сетей для определения и распознавания образов. Она позволяет описать и моделировать вероятностные закономерности, что позволяет повысить точность распознавания и обработки информации.
3. Компьютерное зрение: Математическая модель проекции гаусса применяется для анализа и обработки изображений в области компьютерного зрения. Она позволяет сглаживать шумы и дефекты на изображении, выделять и распознавать объекты, а также оценивать их форму и размеры.
4. Прогнозирование и моделирование: Модель гауссовой проекции часто используется в статистическом анализе и прогнозировании для моделирования и прогнозирования случайных процессов, таких как финансовые рынки, погода, демографические данные и другие. Она позволяет оценивать и прогнозировать вероятности и распределения событий.
5. Медицинская диагностика: Модель гауссовой проекции применяется в медицинской диагностике для анализа и обработки медицинских данных. Она позволяет выявлять и оценивать вероятность различных заболеваний и состояний пациентов на основе статистического анализа клинических данных.
Это лишь некоторые примеры применения математической модели проекции гаусса. Благодаря своей универсальности и эффективности, она находит применение во многих отраслях науки и техники.
Техническая реализация проекции гаусса
Для технической реализации проекции гаусса необходимы некоторые инструменты и алгоритмы. Основная идея проекции гаусса заключается в том, чтобы сократить размерность данных и учесть все важные характеристики распределения.
Одним из основных инструментов, используемых для проекции гаусса, является метод главных компонент (Principal Component Analysis, PCA). Он позволяет сократить размерность данных, выделяя главные компоненты, которые наиболее сильно коррелируют с данными. Этот метод позволяет учесть основные характеристики данных и выделить наиболее значимые компоненты.
Для реализации проекции гаусса также могут использоваться различные алгоритмы машинного обучения, такие как оптимальная фильтрация, фильтр Калмана, нейронные сети и другие. Они позволяют учесть сложные зависимости в данных, которые могут быть упущены при применении простых статистических методов.
Один из важных аспектов технической реализации проекции гаусса - это выбор оптимальных параметров для алгоритмов. Например, при использовании метода главных компонент нужно определить, сколько компонент оставить после сокращения размерности данных. Это можно сделать с помощью критериев информационного критерия Акаике или байесовской информационной критерий.
Важно отметить, что реализация проекции гаусса требует больших вычислительных ресурсов и определенного уровня экспертизы в области статистики и машинного обучения. Поэтому важно выбрать наиболее подходящие инструменты и алгоритмы для конкретной задачи и иметь достаточное количество данных для анализа.



