Сумма углов четырехугольной пирамиды — особенности и формула расчета

Четырехугольная пирамида – это геометрическое тело с четырьмя треугольными гранями и одной основанием, которое может быть любой формы. Одним из важных свойств такой пирамиды является сумма углов, образованных ее гранями. Корректное определение этой суммы позволяет решать различные задачи, связанные с геометрией и построением.

Для расчета суммы углов четырехугольной пирамиды можно использовать следующую формулу: S = 360 градусов - угол α - угол β - угол γ, где α, β и γ – углы, образуемые гранями пирамиды. Эта формула основана на том факте, что сумма углов в треугольнике равна 180 градусам.

Важно отметить, что при расчете суммы углов четырехугольной пирамиды необходимо учитывать особенности структуры и формы пирамиды. Ее боковые грани могут быть равнобедренными или разносторонними, что влияет на их углы. Кроме того, пирамида может быть правильной или неправильной, что также влияет на расчет суммы углов. Поэтому перед расчетом необходимо уточнить характеристики пирамиды и применять соответствующие формулы.

Формула расчета суммы углов четырехугольной пирамиды

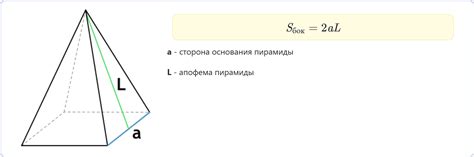
Сумма углов четырехугольной пирамиды может быть рассчитана с помощью формулы, основанной на свойствах геометрических фигур.

Для начала, нужно знать, что четырехугольная пирамида состоит из пяти граней: одной основной и четырех боковых. Основная грань является четырехугольником, а боковые грани - треугольниками.

В четырехугольной пирамиде существует несколько видов углов, которые можно выделить и измерить. Это основные углы, образованные между боковыми гранями пирамиды, углы, образованные между боковыми гранями и основной гранью, и вершина пирамиды.

Для расчета суммы углов четырехугольной пирамиды нужно сложить все углы, входящие в ее состав. В формуле можно выразить это следующим образом:

Сумма углов = углы основного четырехугольника + углы боковых треугольников + угол вершины пирамиды

Углы основного четырехугольника можно измерить, используя соответствующие формулы для четырехугольников.

Углы боковых треугольников могут быть найдены с помощью треугольных функций (например, синуса и косинуса) и измерены в радианах или градусах.

Угол вершины пирамиды, как правило, равен 360° (или 2π радиан), так как он образован тремя плоскими углами в вершине пирамиды.

Итак, сумма углов четырехугольной пирамиды может быть найдена с помощью формулы, учитывающей все углы, образующие эту фигуру.

Общие сведения о четырехугольной пирамиде

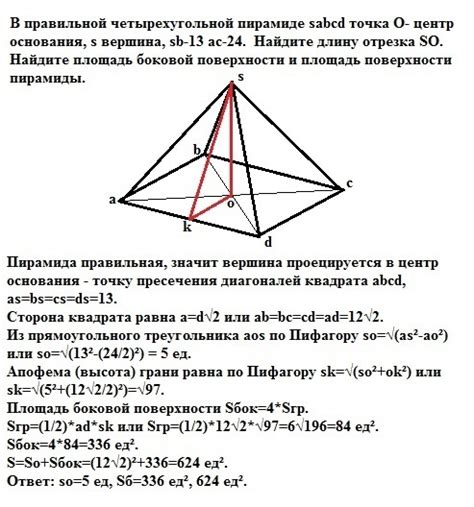
Прямая четырехугольная пирамида – это пирамида, у которой высота, опущенная из вершины на плоскость основания, перпендикулярна этой плоскости. Непрямая четырехугольная пирамида – это пирамида, у которой высота не перпендикулярна плоскости основания.

Регулярная четырехугольная пирамида имеет все стороны основания и все боковые грани равными, а у нерегулярной четырехугольной пирамиды эти меры могут различаться.

Четырехугольная пирамида обладает несколькими особенностями. Например, диагонали основания являются боковыми ребрами пирамиды, а также являются высотами треугольников, образованных пирамидой и его основанием.

Также может быть экваториальная плоскость – плоскость, параллельная основанию пирамиды и делит пирамиду пополам. И полюс – вершина пирамиды, противоположная экваториальной плоскости.

Изучение четырехугольной пирамиды имеет широкое применение в геометрии, физике и строительстве. Знание основных данных и свойств поможет понять структуру и характеристики этого геометрического тела, а также применить его в практических задачах.

Способы вычисления суммы углов

Существует несколько способов вычисления суммы углов четырехугольной пирамиды:

1. Использование формулы Эйлера: сумма углов всех граней плюс угловая дефицитная мера пирамидальной вершины, равная 2π.
2. Расчет суммы углов каждого типа граней отдельно и последующее их сложение:

• Сумма углов треугольных граней можно вычислить с помощью формулы 180° × (количество треугольных граней - 2).
• Сумма углов прямоугольных граней равняется 360° × (количество прямоугольных граней - 2).
• Сумма углов многоугольных граней рассчитывается по формуле 360° × количество многоугольных граней.

Используя указанные способы, можно точно определить сумму углов четырехугольной пирамиды и использовать эту информацию для различных расчетов и анализов.

Варианты расчета для разных типов пирамид

Расчет суммы углов четырехугольной пирамиды может варьироваться в зависимости от ее типа и характеристик. Рассмотрим основные случаи:

• Прямая четырехугольная пирамида: для расчета суммы углов необходимо сложить меры всех углов основания и вершины. Формула выглядит следующим образом: сумма углов = 360 градусов.
• Наклонная четырехугольная пирамида: в данном случае расчет сложнее, и формула зависит от углов наклона сторон основания и вершины. Определение суммы углов осуществляется путем сложения мер углов наклона каждой стороны, а также меры угла вершины.
• Равнобедренная четырехугольная пирамида: для такой пирамиды можно применить специальную формулу для расчета суммы углов. Формула выглядит следующим образом: сумма углов = (количество сторон основания - 2) * 180 градусов + 360 градусов.
• Треугольная пирамида: для треугольной пирамиды расчет суммы углов может быть упрощен, так как основание состоит из трех сторон. Формула выглядит следующим образом: сумма углов = 180 градусов.

Важно помнить, что при расчете суммы углов четырехугольной пирамиды необходимо учитывать только внутренние углы, исключая углы наружной поверхности. Также следует учесть, что сумма углов может быть разной в зависимости от выбранных единиц измерения (градусы или радианы), поэтому важно быть внимательным при выборе и применении формулы расчета.

Особенности применения формулы

Расчет суммы углов четырехугольной пирамиды с помощью формулы может быть полезным в различных ситуациях. Однако следует учитывать некоторые особенности применения данной формулы:

1. Формула применима только для четырехугольных пирамид, состоящих из четырех треугольников.
2. Углы пирамиды должны быть измерены в градусах и быть положительными значениями.
3. Формула применяется к каждому треугольнику пирамиды по отдельности, а затем полученные значения суммируются.
4. В случае, если углы треугольника не являются прямыми, сумма углов может быть отличной от 360 градусов.
5. Формула не учитывает дополнительные факторы, такие как несимметричность пирамиды или кривизну поверхности.

При применении данной формулы необходимо учесть указанные особенности и применять ее с осторожностью, учитывая конкретные условия задачи или исследования.