Граф - это абстрактная математическая структура, состоящая из вершин и ребер. Каждое ребро соединяет две вершины, их степень - одно из наиболее важных понятий в теории графов. Степень вершины определяет количество ребер, связанных с данной вершиной. В данной статье мы рассмотрим более подробно, что такое степень вершины графа и как она вычисляется.
Степень вершины - это количество ребер, инцидентных данной вершине. Другими словами, степень вершины показывает, сколько ребер выходит из данной вершины или входит в нее. Например, если вершина имеет степень 3, это означает, что существует три ребра, связанных с данной вершиной.
Степень вершины может быть как положительной, так и нулевой. Положительная степень указывает на наличие ребер, связанных с данной вершиной, а нулевая степень означает отсутствие инцидентных ребер. Важно отметить, что в неориентированном графе степень вершины равна количеству ребер, инцидентных данной вершине, а в ориентированном графе степень вершины делится на две части: степень входа (количество входящих ребер) и степень выхода (количество исходящих ребер).
Что такое степень вершины графа?

Степень вершины обычно обозначается deg(v), где v - вершина графа. Для неориентированного графа, степень вершины равна сумме степеней всех инцидентных ей ребер. Для ориентированного графа, степень вершины разделяется на входящую и исходящую степени, которые указывают на количество входящих и исходящих ребер соответственно.
Степень вершины графа может быть использована для анализа и классификации графов. Например, вершины с нулевой степенью (изолированные вершины) являются неподвижными элементами графа, не имеющими связей с другими вершинами. Вершины с минимальной степенью могут быть использованы для поиска главных компонентов графа, а вершины с максимальной степенью могут играть важную роль в распределении информации в сети.
Примером степени вершины может быть следующая ситуация: у нас есть граф, представляющий сеть дорог города. Вершины графа представляют перекрестки, а ребра - дороги между перекрестками. Степень вершины в этом случае будет указывать на количество дорог, связанных с определенным перекрестком. Например, если степень вершины равна 3, это означает, что у данного перекрестка есть три входящие или исходящие дороги.
Описание понятия

Степенью вершины графа называется количество ребер, которые связывают данную вершину с остальными вершинами графа.
Другими словами, степень вершины графа показывает, сколько "соседей" имеет данная вершина, то есть сколько вершин примыкает к ней в графе.
Степень вершины может быть полезной характеристикой в анализе графов. Она может помочь определить центральность и важность вершин в графе. Также можно использовать степень вершины для решения различных задач, связанных с графами, например, для поиска наиболее важных вершин или для обнаружения сообществ или подграфов в большом графе.
Степень вершины может быть как исходящей (количество ребер, исходящих из вершины), так и входящей (количество ребер, входящих в вершину). В некоторых случаях может быть также важно учитывать взвешенность ребер при определении степени вершины.
Примеры степеней вершин графа:
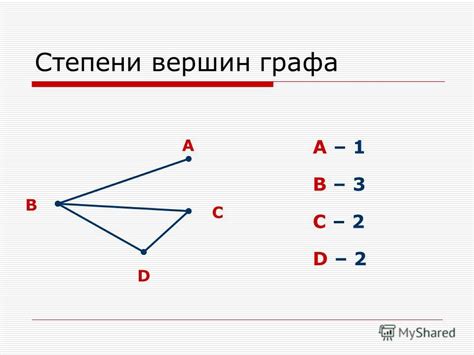
- Вершина A имеет степень 3, так как к ней примыкают 3 ребра;
- Вершина B имеет степень 2;
- Вершина C имеет степень 1;
- Вершина D имеет степень 2.
Степень вершины в ориентированных графах
Степень вершины в ориентированном графе определяется количеством исходящих и входящих рёбер, связанных с данной вершиной.
Исходящая степень (также называемая исходящей степенью) вершины в ориентированном графе определяется количеством рёбер, идущих из данной вершины в другие вершины графа. Обозначается обычно как outdegree(v), где v – вершина.
Входящая степень (также называемая входящей степенью) вершины в ориентированном графе определяется количеством рёбер, входящих в данную вершину из других вершин графа. Обозначается обычно как indegree(v), где v – вершина.
Сумма исходящей и входящей степеней вершины в ориентированном графе равна общей степени данной вершины и называется полустепенью. Обозначается обычно как degree(v), где v – вершина.
Например, в ориентированном графе с вершинами A, B и C и рёбрами (A, B), (A, C), (B, C), (C, B), исходящая степень вершины A равна 2, входящая степень равна 0, а полустепень равна 2.
| Вершина | Исходящая степень | Входящая степень | Полустепень |
|---|---|---|---|
| A | 2 | 0 | 2 |
| B | 1 | 1 | 2 |
| C | 1 | 2 | 3 |
Степень вершины в неориентированных графах

Степенью вершины в неориентированном графе называется количество ребер, инцидентных данной вершине. Другими словами, это количество соседей у данной вершины.
Если в графе есть вершины, у которых степень равна 0, то они называются изолированными вершинами. Это означает, что эти вершины не имеют соседей и не связаны ни с одной другой вершиной.
Степень вершины может быть как конечной, так и бесконечной. Например, в бесконечном графе, представляющем числовую прямую, степень любой вершины будет бесконечной.
Степень вершины имеет особое значение в анализе графов. Она может использоваться, например, для определения центральности вершины в графе – насколько она важна и центральна среди других вершин. Более высокая степень может указывать на более активное взаимодействие с другими вершинами графа.
Примеры:
Рассмотрим простой граф, состоящий из 5 вершин и 6 ребер:
Степени вершин в этом графе:
- Вершина A имеет степень 2, так как инцидентна 2 ребрам.
- Вершина B также имеет степень 2.
- Вершина C имеет степень 3.
- Вершина D имеет степень 1.
- Вершина E также имеет степень 1.
Таким образом, степени вершин в данном графе состоят из чисел 1, 2 и 3.
Примеры степеней вершин в графах

Степень вершины в графе определяется как количество ребер, которые инцидентны данной вершине. Знание степеней вершин позволяет анализировать свойства графов и выявлять интересные связи. Вот несколько примеров степеней вершин в графах:
Пример 1:
Рассмотрим простой граф с тремя вершинами и тремя ребрами, соединяющими эти вершины. Каждая вершина имеет степень 2, так как у каждой вершины есть ровно два соседних узла.
Пример 2:
Предположим, что у нас есть граф с пятью вершинами и шестью ребрами. Вершина A связана с вершинами B, C и E, поэтому ее степень равна 3. Вершины B и C связаны с вершиной A и, кроме того, соединены друг с другом, поэтому их степени равны 2. Вершины D и E также имеют степень 2.
Пример 3:
Рассмотрим следующий граф, содержащий три вершины и два ребра. Здесь каждая вершина имеет степень 1, так как она соединена только с одной другой вершиной.
Таким образом, степень вершин в графах может различаться в зависимости от количества ребер, инцидентных данным узлам.
Как определить степень вершины графа?

Старайтесь соблюдать последовательность шагов при определении степени вершины графа:
- Проанализируйте все ребра, связанные с данной вершиной.
- Подсчитайте количество этих ребер. Это и будет степенью вершины.
Например, рассмотрим граф, представленный следующей таблицей:
| Вершина | Смежные Ребра |
|---|---|
| A | B, C, D |
| B | A, C |
| C | A, B, D |
| D | A, C |
Если мы хотим определить степень вершины B, мы смотрим на все ребра, связанные с вершиной B, и видим, что это ребра AB и BC. Значит, степень вершины B равна 2.
Теперь, если мы хотим определить степень вершины C, мы смотрим на все ребра, связанные с вершиной C, и видим, что это ребра AC, BC и CD. Значит, степень вершины C равна 3.
Таким образом, зная все ребра, связанные с вершиной, можно легко определить ее степень в графе.
Зависимость степени вершины от свойств графа
Степень вершины в графе может зависеть от различных свойств этого графа. Важность этих свойств может варьироваться в зависимости от применяемого алгоритма или области, в которой рассматривается графовая структура.
Одним из основных свойств графа, влияющих на степень вершины, является его тип. В ориентированных графах степень вершины определяется как сумма входящих и исходящих ребер, в то время как в неориентированных графах степень вершины равна количеству инцидентных ей ребер. Таким образом, степень вершины может отличаться в зависимости от того, является ли граф ориентированным или нет.
Еще одной важной характеристикой графа, оказывающей влияние на степень вершины, является его плотность. Плотность графа определяется как отношение количества ребер к количеству возможных ребер в графе. Если граф имеет высокую плотность, то вероятность того, что вершина будет иметь большую степень, также повышается.
Еще одним важным фактором, влияющим на степень вершины, является структура графа. Например, в случае деревьев каждая вершина, кроме корня, имеет степень равную 1, тогда как у корня степень может быть равна 0 (если он является листом) или больше 1 (если у него есть дети). В случае графов с циклами, степень вершины может варьироваться в зависимости от количества и конфигурации циклов в графе.
Таким образом, степень вершины в графе зависит от нескольких факторов, включая тип графа (ориентированный или неориентированный), его плотность и структуру. Учет этих факторов может быть необходим при анализе и обработке графовых данных.







