Среднее арифметическое - одна из основных математических операций, которая позволяет найти среднее значение двух чисел. Она широко используется во многих областях, включая физику, статистику, экономику и многие другие.
Понимание того, как составляется среднее арифметическое, важно для решения широкого спектра задач. Простой пример - нахождение среднего значения двух чисел. Чтобы найти это значение, нужно сложить два числа и разделить полученную сумму на два.
Формула для нахождения среднего арифметического двух чисел:
(a + b) / 2
Где a и b - исходные числа, а / - символ деления.
К примеру, чтобы найти среднее арифметическое чисел 5 и 9, нужно сложить эти числа (5 + 9 = 14) и разделить полученную сумму на 2 (14 / 2 = 7). Таким образом, среднее арифметическое чисел 5 и 9 равно 7.
Что такое среднее арифметическое чисел?

Формула для вычисления среднего арифметического двух чисел представляет собой простое деление суммы двух чисел на 2:
| Сумма чисел | Среднее арифметическое = ----------------- |
| Количество чисел | Число 1 + Число 2 |
| ----------------- | |
| 2 |
Среднее арифметическое может быть полезно для оценки типичного значения в наборе чисел, а также для сравнения значений и определения отклонений от среднего.
Например, если у нас есть два числа: 5 и 8, мы можем вычислить их среднее арифметическое следующим образом:
| Сумма чисел | Среднее арифметическое = ----------------- |
| 5 + 8 | ----------------- |
| 2 | |
| 13 | ----------- = 6.5 |
| 2 |
Таким образом, среднее арифметическое чисел 5 и 8 равно 6.5.
Как вычисляется среднее арифметическое?

Формула для вычисления среднего арифметического двух чисел выглядит следующим образом:
| Число 1 | Число 2 | Среднее арифметическое |
|---|---|---|
| a | b | (a + b) / 2 |
Для вычисления среднего арифметического, необходимо сложить значения двух чисел и разделить полученную сумму на 2. Например, если число 1 равно 5, а число 2 равно 8, то среднее арифметическое будет равно (5 + 8) / 2 = 6.5.
Принципы вычисления среднего арифметического

- Сложение: Для получения среднего арифметического двух чисел, необходимо их сумму разделить на 2.
- Усреднение: Среднее арифметическое позволяет найти значение, которое находится между двумя числами и равно сумме этих чисел, деленной на их количество.
- Равномерность: При вычислении среднего арифметического, каждое число имеет одинаковую важность и вносит равный вклад.
Формула для вычисления среднего арифметического двух чисел:
Среднее арифметическое = (число 1 + число 2) / 2
Например, для чисел 5 и 7:
Среднее арифметическое = (5 + 7) / 2 = 6
Таким образом, среднее арифметическое двух чисел равно 6.
Формула для вычисления среднего арифметического

Среднее арифметическое двух чисел можно вычислить с помощью простой формулы. Для этого необходимо сложить эти два числа и разделить полученную сумму на 2.
Формула для вычисления среднего арифметического двух чисел имеет следующий вид:
(число1 + число2) / 2
Где число1 и число2 - два заданных числа, а + и / означают соответственно сложение и деление.
Применение данной формулы позволяет быстро и легко вычислить среднее арифметическое двух чисел, не требуя от пользователя дополнительных математических навыков.
Например, для двух чисел 5 и 9, среднее арифметическое будет:
(5 + 9) / 2 = 7
Таким образом, среднее арифметическое чисел 5 и 9 равно 7.
Примеры вычисления среднего арифметического:

Давайте рассмотрим несколько примеров вычисления среднего арифметического двух чисел:
- Пример 1: Вычисление среднего арифметического чисел 2 и 6:
Сумма чисел 2 и 6 равна 8.
Чтобы найти среднее арифметическое, нужно разделить сумму чисел на их количество, то есть 8 на 2:
8 ÷ 2 = 4
Среднее арифметическое чисел 2 и 6 равно 4.
- Пример 2: Вычисление среднего арифметического чисел 10 и 15:
Сумма чисел 10 и 15 равна 25.
Чтобы найти среднее арифметическое, нужно разделить сумму чисел на их количество, то есть 25 на 2:
25 ÷ 2 = 12.5
Среднее арифметическое чисел 10 и 15 равно 12.5.
- Пример 3: Вычисление среднего арифметического чисел -3 и 9:
Сумма чисел -3 и 9 равна 6.
Чтобы найти среднее арифметическое, нужно разделить сумму чисел на их количество, то есть 6 на 2:
6 ÷ 2 = 3
Среднее арифметическое чисел -3 и 9 равно 3.
Значение и применение среднего арифметического
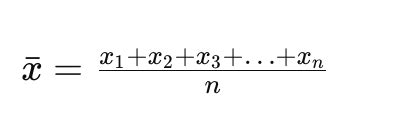
Значение среднего арифметического применяется во многих областях, начиная от математики и статистики, и заканчивая экономикой, физикой, искусственным интеллектом и множеством других наук и практических сфер деятельности. Вычисление среднего арифметического позволяет получить обобщенное представление о данных и он является одним из базовых инструментов анализа и интерпретации информации.
Кроме того, среднее арифметическое применяется для выявления трендов и изменений в данных, а также для сравнения и оценки различных значений. Например, в экономике среднее арифметическое может быть использовано для определения инфляции или роста заработной платы. А в области машинного обучения, это значение может служить для установления границ и классификации данных в задачах распознавания образов или прогнозирования.
Важные моменты при использовании среднего арифметического
1. Учет всех значений: При расчете среднего арифметического необходимо учесть все значения, включая отрицательные и нулевые числа. Пропуск или исключение некоторых значений может исказить результат.
2. Обработка выбросов: Если в множестве чисел имеются выбросы, то они могут сильно повлиять на значение среднего арифметического. В таких случаях целесообразно использовать другие статистические меры, например, медиану.
3. Взвешенное среднее: Если числа в множестве имеют различную важность или вес, то следует использовать взвешенное среднее. Взвешенное среднее учитывает вес каждого значения и позволяет более точно отобразить значимость каждого числа.
4. Компоненты несопоставимы остальным множеством: В некоторых случаях может потребоваться исключить из расчетов значения, которые являются аномальными или несопоставимыми остальным множеством. Например, при сравнении уровня образования в разных странах может быть исключено значение страны, которая значительно отклоняется от среднего.
Важно использовать среднее арифметическое с учетом этих моментов, чтобы получить максимально достоверный и репрезентативный результат. Использование этой статистической меры может быть полезным в различных областях, от экономики и финансов до анализа данных и научных исследований.



