Математика и алгебра являются фундаментальными дисциплинами, изучающими различные виды функций. Одним из таких видов функций являются кубические функции, которые обладают особыми свойствами и интересными графиками.
В данной статье мы рассмотрим две кубические функции - fx(x) и gx(x) - и проведем их сравнительный анализ. Отличия и сходства между ними помогут нам лучше понять эти функции и их поведение на графиках.
Функция fx(x) имеет общий вид f(x) = ax^3 + bx^2 + cx + d, где a, b, c, d - коэффициенты. Она является кубической функцией с переменными коэффициентами. В зависимости от значений коэффициентов, график функции может иметь различные формы - от положительно выпуклого до отрицательно выпуклого. Также функция может иметь один, два или три действительных корня.
Сравнение функций fx(x) и gx(x) в кубе
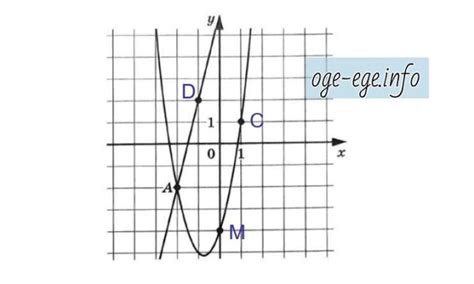
Функция fx(x) представляет собой функцию, определённую на промежутке [a, b], где a и b – константы, и является кубической функцией. Её график имеет форму параболы, и ветви этой параболы направлены вверх или вниз, в зависимости от значений a и b. Функция fx(x) может принимать положительные и отрицательные значения в зависимости от значения аргумента x.
Функция gx(x) также является кубической функцией, но имеет свои уникальные свойства. Её график имеет форму параболы с выпуклостью вверх или вниз, в зависимости от значений её коэффициентов. В отличие от функции fx(x), функция gx(x) может иметь точки перегиба, где её кривизна меняется. Такие точки могут оказаться ключевыми для определения поведения функции в определённом промежутке.
Сравнение функций fx(x) и gx(x) позволяет выявить их сходства и различия. Обе функции являются кубическими функциями и имеют параболоидную форму графика. Однако, функция gx(x) может иметь дополнительные точки перегиба и, следовательно, более сложную кривизну. Кроме того, функция fx(x) может быть ограничена своими значениями a и b, что может повлиять на её поведение в определённых интервалах.
В итоге, сравнение функций fx(x) и gx(x) в кубе позволяет более полно оценить их свойства и понять, как они могут использоваться в различных задачах и сферах математики.
Описание функции fx(x) в кубе
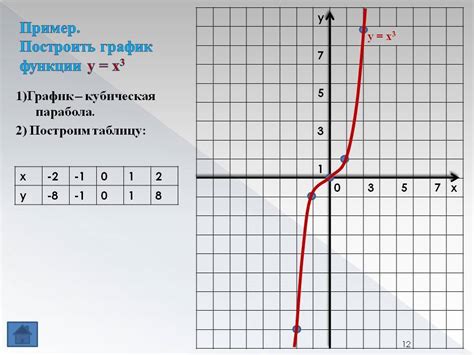
Функция fx(x) в кубе представляет собой математическую функцию, которая вычисляет третью степень числа x. То есть, результатом функции будет число, полученное путем возведения x в куб.
Данная функция может быть представлена следующим образом:
fx(x) = x * x * x
Где:
- fx(x) - обозначение функции fx для конкретного значения x.
- x - аргумент функции, число, которое будет возведено в куб.
Например, для значения x = 2, функция fx(x) возвращает результат:
fx(2) = 2 * 2 * 2 = 8
Таким образом, функция fx(x) в кубе является простым способом для возведения числа в куб и может быть использована в различных математических вычислениях и задачах.
Описание функции gx(x) в кубе
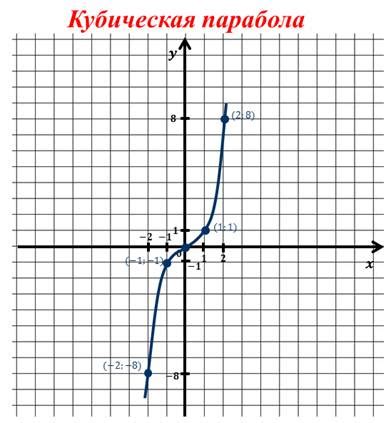
При анализе функции gx(x) в кубе необходимо обратить внимание на такие характеристики, как:
- Область определения: функция gx(x) в кубе определена для всех действительных значений x. Это означает, что любое действительное число может быть подставлено в функцию и получить результат.
- Область значений: значения функции gx(x) в кубе также принадлежат множеству действительных чисел. Следовательно, результатом функции может быть любое действительное число.
- График: график функции gx(x) в кубе образует параболоид с вершиной в начале координат (0, 0, 0). Он симметричен относительно оси Oy.
- Производная: производная функции gx(x) в кубе равна gx'(x) = 3x^2. Это означает, что скорость изменения функции gx(x) в кубе будет увеличиваться с ростом значения x.
- Интеграл: интеграл функции gx(x) в кубе равен Gx(x) = (1/4)x^4 + C, где C - произвольная постоянная.
Функция gx(x) в кубе используется в различных областях науки и техники, включая физику, экономику, статистику, программирование и др. Ее свойства и особенности делают ее полезной для моделирования и решения широкого спектра задач.
Обзор функций fx(x) и gx(x) в кубе
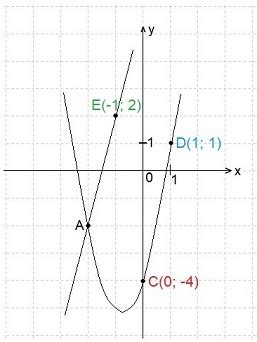
Функция gx(x) в кубе также является кубической функцией, но отличается от fx(x) своим коэффициентом. Её можно записать в виде gx(x) = a * x^3, где a - коэффициент.
В общем случае, обе функции являются гладкими и монотонно возрастающими на всей области определения. Они обладают симметрией относительно начала координат и оси Oy.
Функции fx(x) и gx(x) в кубе часто используются в математическом анализе и других областях науки, для моделирования различных процессов и явлений, а также в построении графиков.
Сравнение fx(x) и gx(x) в кубе позволяет выявить различия в их поведении и эффекты, которые они оказывают на исследуемый объект. Это может быть полезно при анализе данных и прогнозировании результатов.
Примеры использования функции fx(x) в кубе
Функция fx(x) в кубе может быть использована в различных областях, включая математику, физику, экономику и программирование. Ниже приведены некоторые примеры использования функции fx(x) в различных областях:
- В математике, функция fx(x) в кубе может использоваться для нахождения объема куба. Формула для вычисления объема куба с помощью функции fx(x) выглядит следующим образом: V = fx(x) = x^3, где x - длина ребра куба.
- В физике, функция fx(x) в кубе может использоваться для моделирования свойств и поведения объектов с трехмерной формой. Например, можно использовать функцию fx(x) для описания изменения объема газа или для моделирования движения тела в трехмерном пространстве.
- В экономике, функция fx(x) в кубе может использоваться для моделирования зависимости между тремя переменными. Например, функция fx(x) может моделировать зависимость объема производства от затрат производства и цены товара.
- В программировании, функция fx(x) в кубе может использоваться для решения задач, связанных с трехмерной графикой, виртуальной реальностью и моделированием. Например, функция fx(x) может использоваться для создания трехмерных эффектов или анимации в играх и приложениях.



