Синус – одна из основных тригонометрических функций, которая широко используется в геометрии, физике, астрономии и других научных дисциплинах. Синусное значение возникает при измерении угла между горизонтальной осью и наклонной стороной треугольника. Однако синусом также можно оперировать и в случае, когда треугольник не является прямоугольным.
Несмотря на то что обсчет синуса для не прямоугольного треугольника более сложен, существует формула, которая позволяет его вычислить. В отличие от прямоугольного треугольника, где синус считается по отношению высоты к гипотенузе, для не прямоугольного треугольника синус определяется как отношение длины противоположной стороны к длине гипотенузы.
Формула для расчета синуса не прямоугольного треугольника:
sin(угол A) = противоположная сторона / гипотенуза
Что такое синус не прямоугольного треугольника?
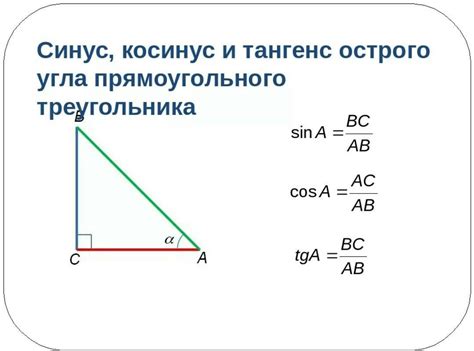
Синус обозначается символом sin и используется в геометрии и тригонометрии для вычисления различных параметров треугольника.
Для нахождения значения синуса не прямоугольного треугольника необходимо знать длины сторон треугольника и угол между этими сторонами.
Формула для вычисления синуса треугольника:
sin(угол А) = противоположная сторона / гипотенуза
Синус не прямоугольного треугольника имеет значения в интервале от -1 до 1. Когда угол равен 90 градусов, синус равен 1, а когда угол равен 0 градусов, синус равен 0.
Знание синуса не прямоугольного треугольника помогает в решении различных геометрических и физических задач, а также находит применение в технических расчетах и конструкциях.
Определение синуса не прямоугольного треугольника
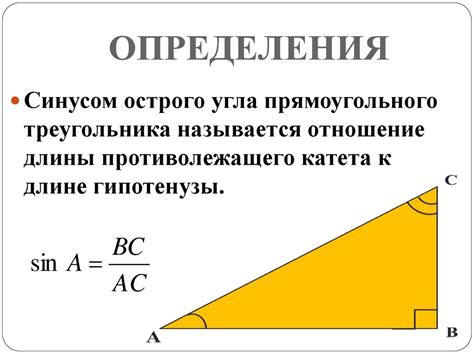
Формула синуса для не прямоугольного треугольника устанавливает соотношение между противолежащим катетом и соответствующим ему углом. Синус угла A в любом треугольнике вычисляется по формуле:
sin(A) = (a / c)
где:
- sin(A) - синус угла A
- a - противолежащий катет
- c - гипотенуза (длина наибольшей стороны треугольника)
Данная формула позволяет вычислить синус угла в не прямоугольном треугольнике, зная длину противолежащего катета и гипотенузы. Коэффициентом перед противолежащим катетом является sin(A), который представляет собой отношение сторон треугольника.
Таким образом, зная длину противолежащего катета и длину гипотенузы, можно легко вычислить синус угла и получить значение этой тригонометрической функции для не прямоугольного треугольника.
Формула для расчета синуса не прямоугольного треугольника
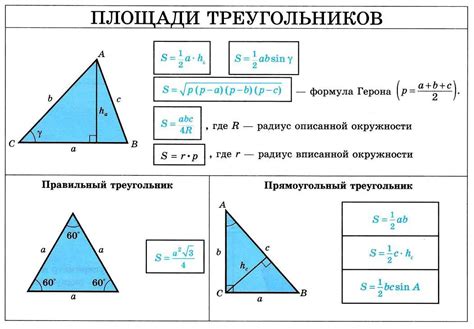
Для расчета синуса не прямоугольного треугольника с известными сторонами и углами применяется следующая формула:
- Найдите длины всех сторон треугольника.
- Найдите значение полупериметра треугольника:
- Используя формулу полупериметра и значения сторон треугольника, найдите площадь треугольника:
- Найдите значение радиуса вписанной окружности треугольника:
- Найдите значение синуса центрального угла треугольника:
$$p = \frac{{a + b + c}}{2}$$
$$S = \sqrt{{p(p - a)(p - b)(p - c)}}$$
$$r = \frac{{S}}{{p}}$$
$$\sin(A) = \frac{{a}}{{2r}}$$
После выполнения всех вышеперечисленных шагов, получите значение синуса центрального угла треугольника. Важно отметить, что для расчета всех величин треугольника необходимо знать значения сторон и углов.



