Учебный курс математики для первоклассников начинается с первых шагов в мире чисел. Соразмерно возрасту детей, он включает в себя базовые концепции и понятия, которые позволяют учащимся понимать мир числовых значений и использовать их в повседневной жизни. Один из основных аспектов, которому уделяется внимание, - это разбор и состав чисел.
Состав числа – это разложение числа на составляющие его части. Первоклассники учатся анализировать и понимать, что каждая цифра в числе имеет свое значение и место. Возможность разбирать число на составляющие и строить на его основе другие числа является ключевым фундаментом для дальнейшего математического развития.
Например, число 54 может быть разложено на 50 и 4, где первая цифра представляет десятки, а вторая – единицы. То есть, число 54 состоит из 5 десятков и 4 единиц. Такой подход не только помогает учащимся усвоить материал, но и способствует развитию логического мышления и представления о структуре чисел.
Число как составная величина

Например, число 345.67 состоит из трех цифр: 3, 4 и 5, а также имеет разделительный знак – точку, который обозначает разделение целой и десятичной части числа.
В состав числа также могут входить другие символы или знаки. Например, знак минус (-) может использоваться для обозначения отрицательных чисел.
Чтобы правильно идентифицировать и анализировать числа, необходимо знать их состав и значение каждой составляющей. Это позволяет выполнять различные математические операции, такие как сложение, вычитание, умножение и деление чисел.
Осознание того, что число представляет собой составную величину, помогает учащимся лучше понимать и использовать числа в повседневной жизни. Они могут использовать это знание для работы с деньгами, измерения времени, решения задач и многих других ситуаций, где числа играют важную роль.
Числа в повседневной жизни

Числа окружают нас повсюду в нашей повседневной жизни. Мы видим и используем их в самых разных ситуациях: при счете денег, измерении времени, определении пройденного расстояния и многом другом.
Например, когда мы идем в магазин, у нас есть определенное количество денег, которое мы можем потратить. Мы считаем цены на товары, складываем их в уме или с помощью калькулятора, чтобы знать, сколько денег у нас останется.
Также мы используем числа для определения времени. Например, мы знаем, что уроки в школе длительностью 45 минут, а перемены между уроками 10 минут. Мы смотрим на часы или будильник, чтобы знать, когда нужно идти в школу или на работу, когда начинается и заканчивается урок или смена.
Кроме того, мы используем числа для определения пройденного расстояния. Если мы едем на автобусе или поезде, мы знаем, на какой остановке нужно выходить, потому что знаем номер остановки или количество остановок до нужной нам.
В нашей повседневной жизни мы также используем числа для сравнения и оценки. Например, мы оцениваем количество мест в кинотеатре, чтобы знать, насколько мест будет достаточно для всех желающих. Мы сравниваем размеры одежды или обуви, чтобы выбрать подходящий нам размер.
Таким образом, числа играют важную роль в нашей повседневной жизни. Они помогают нам ориентироваться, считать, сравнивать и принимать решения. Знание и понимание чисел помогает нам лучше адаптироваться к миру и быть успешными в различных сферах нашей жизни.
Число как модель предмета

Представьте, что у вас есть 3 яблока. Вы можете расставить их перед собой и посчитать каждое яблоко. В результате получится число 3. В этом случае число 3 является моделью предметов - яблок.
Таким же образом можно представить любое другое число. Например, если у вас есть 5 карандашей, то число 5 становится моделью предметов - карандашей. Или если у вас есть 7 игрушек, то число 7 становится моделью предметов - игрушек.
Понимание числа как модели предмета помогает учащимся первого класса не только освоить базовые математические понятия, но и применять их в повседневной жизни. Умение считать предметы, определять их количество и сравнивать их, является важным знанием для развития логического мышления и математических навыков.
Сложение чисел

Для сложения чисел нужно помнить несколько правил:
- Если сложить два положительных числа, получится положительное число.
- Если сложить два отрицательных числа, получится отрицательное число.
- Если сложить отрицательное и положительное число, нужно вычитать по модулю и приписывать знак числа с большей абсолютной величиной.
Например, чтобы сложить числа 3 и 5, нужно записать их подряд и приписать знак "+" между ними:
| 3 | + | 5 |
Затем, складывая числа по очереди, получаем сумму:
| 3 | + | 5 | = | 8 |
Таким образом, сумма чисел 3 и 5 равна 8.
Сложение чисел является одной из основных арифметических операций и широко используется в повседневной жизни.
Определение сложения
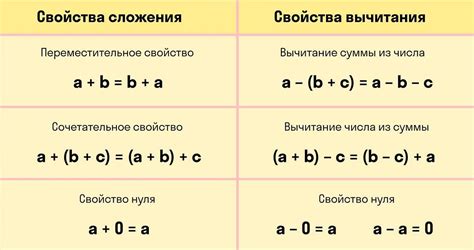
Например, если сложить числа 5 и 3, то получится сумма 8. Можно записать это так: 5 + 3 = 8.
В процессе сложения, первое число называется первым слагаемым, второе число - вторым слагаемым, а сумма - результатом сложения. Порядок слагаемых не важен, так как сложение коммутативное свойство. То есть, результат сложения двух чисел будет таким же, независимо от порядка их расположения: 5 + 3 = 3 + 5 = 8.
Сложение можно представить с помощью различных предметов или иллюстраций, чтобы ученикам было более понятно. Например, можно использовать счетные палочки или картинки с изображением предметов, чтобы показать, что при сложении объединяются две группы предметов в одну большую группу.
Примеры сложения чисел
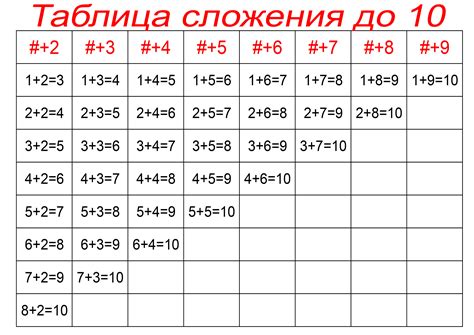
Пример 1:
Сложи числа 3 и 4:
3 + 4 = 7
Пример 2:
Сложи числа 5 и 2:
5 + 2 = 7
Пример 3:
Сложи числа 8 и 6:
8 + 6 = 14



