Сочетательный закон сложения 2 класс - это одно из основных правил комбинаторики, которое используется при решении задач связанных с подсчетом количества различных комбинаций. Понимание и применение этого закона является важным элементом успешного решения задач, связанных с анализом вероятности и количественного подсчета в математике.
Суть сочетательного закона сложения 2 класс заключается в следующем: если имеется два непересекающихся множества объектов, причем первое множество содержит m объектов, а второе - n объектов, то общее количество комбинаций получается прибавлением числа объектов обоих множеств.
Примером применения сочетательного закона сложения 2 класс может быть ситуация, когда у нас есть m разных орехов и n разных яблок на выбор, и мы хотим посчитать количество комбинаций, которые можно составить, взяв один объект из каждого множества. Исходя из закона сложения, общее количество возможных комбинаций будет равно m + n.
Сочетательный закон сложения 2 класс: ключевые аспекты и его значение
Ключевыми аспектами сочетательного закона сложения второго класса являются:
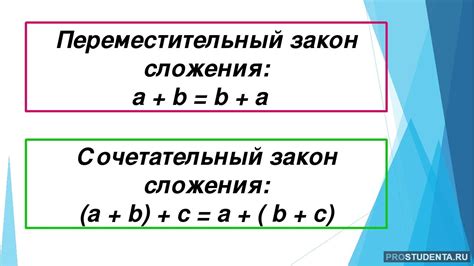
- Коммутативность - порядок слагаемых не влияет на сумму. Например, 2 + 3 + 4 = 4 + 3 + 2 = 9.
- Ассоциативность - группировка слагаемых не влияет на сумму. Например, (2 + 3) + 4 = 2 + (3 + 4) = 9.
- Нейтральный элемент - прибавление нуля не изменяет число. Например, 2 + 0 = 2.
Сочетательный закон сложения второго класса имеет важное значение в математике, так как позволяет упрощать вычисления и работать с числами более удобным способом. Он является основой для более сложных математических операций и концепций.
Основные принципы сочетательного закона сложения 2 класс

Основной принцип сочетательного закона сложения второго класса заключается в том, что сумма трех чисел не зависит от порядка их сложения. Независимо от того, какое число будет сложено первым, результат останется неизменным.
Например, если мы имеем числа 5, 7 и 9, то при сложении в любом порядке, результат будет одинаковым. Если мы сложим сначала 5 и 7, а затем прибавим 9, то получим сумму 21. Если мы сначала сложим 7 и 9, а затем прибавим 5, то результат также будет равен 21.
Этот принцип работает не только для трех чисел, но и для любого количества чисел. Независимо от порядка их сложения, сумма всегда будет одинаковой.
Сочетательный закон сложения второго класса является ключевым в алгебре и имеет большое практическое значение. Он позволяет легко выполнять арифметические операции и облегчает работу с числами.
Примеры применения сочетательного закона сложения 2 класс

Сочетательный закон сложения в математике используется для вычисления суммы двух или более чисел. Данный закон позволяет нам упростить вычисления и сделать их более легкими и понятными.
Давайте рассмотрим несколько примеров:
1. У Маши есть 3 красных шарика, а у Пети - 2 синих шарика. Сколько всего шариков у них вместе? По сочетательному закону сложения мы складываем количество красных шариков и количество синих шариков: 3 + 2 = 5. Ответ: у Маши и Пети вместе 5 шариков.
2. На столе лежит 4 яблока, а в корзине - 3 яблока. Сколько яблок всего? Используя сочетательный закон сложения, мы складываем количество яблок на столе и в корзине: 4 + 3 = 7. Ответ: всего 7 яблок.
3. В школьной библиотеке 6 книг по математике и 2 книги по физике. Сколько всего книг в библиотеке? Применяя сочетательный закон сложения, мы складываем количество книг по математике и количество книг по физике: 6 + 2 = 8. Ответ: в библиотеке всего 8 книг.
Таким образом, сочетательный закон сложения 2 класс позволяет нам удобно и быстро складывать числа и находить их сумму. Это очень полезный навык, который поможет решать разнообразные математические задачи и применять их в повседневной жизни.
Значение сочетательного закона сложения 2 класс в математике
Согласно сочетательному закону сложения, результат сложения двух чисел не изменяется, если поменять их местами. Другими словами, при сложении двух чисел, порядок слагаемых можно менять, и результат останется тем же.
Для лучшего понимания сочетательного закона сложения, можно представить это на примере. Пусть у нас есть два числа, а и б. Если мы сложим их в порядке а + б, то получим сумму. Но если поменяем местами слагаемые и сложим их в порядке б + а, то результат будет таким же.
| а | б | а + б | б + а |
| 3 | 5 | 3 + 5 = 8 | 5 + 3 = 8 |
| 7 | 2 | 7 + 2 = 9 | 2 + 7 = 9 |
| 4 | 9 | 4 + 9 = 13 | 9 + 4 = 13 |
Из таблицы видно, что результат сложения остается неизменным независимо от порядка слагаемых. Это и есть суть сочетательного закона сложения 2 класс.
Использование сочетательного закона сложения упрощает работу с числами и помогает в быстром подсчете результатов сложений. Также он играет важную роль в более сложных операциях алгебры, где суммирование играет важную роль.
Математические связи сочетательного закона сложения 2 класс

Этот закон можно проиллюстрировать на примере с числами:
- 10 + 5 = 15
- 5 + 10 = 15
Как видно из примера, порядок слагаемых (10 и 5) не влияет на сумму, которая в обоих случаях равна 15.
Сочетательный закон сложения можно представить в виде следующей формулы:
a + b = b + a
где a и b - любые числа. Эта формула демонстрирует, что порядок слагаемых можно менять без изменения суммы.
Использование сочетательного закона сложения упрощает вычисления и позволяет упорядочить слагаемые по удобству. Дети второго класса изучают этот закон и применяют его при выполнении математических задач, чтобы более эффективно решать примеры и понимать основы сложения.



