Синус – это одна из основных тригонометрических функций, которая находит широкое применение в математике, физике, инженерии и других науках. Она представляет собой отношение длины противолежащего катета к длине гипотенузы в прямоугольном треугольнике. Синус обычно обозначается символом sin и может принимать значения от -1 до 1.
Синус играет важную роль в решении различных задач, связанных с измерением углов, колебаниями, периодическими функциями и пространственными векторами. Он широко используется при моделировании и анализе изменений в физических и математических системах.
Для использования синуса правильно необходимо знать его основные свойства и формулы, а также уметь применять их на практике. Помимо прямого использования, синус также является основой для других тригонометрических функций, таких как косинус, тангенс и котангенс.
Синус: основная информация и применение

Синус широко применяется в различных областях, включая науку, инженерию и физику. Он используется для моделирования и анализа колебаний, таких как звук и свет, и является важным инструментом в теории сигналов и систем. Благодаря своим свойствам, синус может быть использован для описания и предсказания различных физических явлений, таких как звуковые и световые волны, электрические и магнитные поля, а также многие другие.
Синус также находит широкое применение в математике и статистике. Он используется для решения уравнений, моделирования траекторий, аппроксимации данных и анализа различных математических функций. Благодаря своей периодичности и гладкости, синус также используется в численных методах, финансовой математике и машинном обучении.
Что такое синус и как он работает
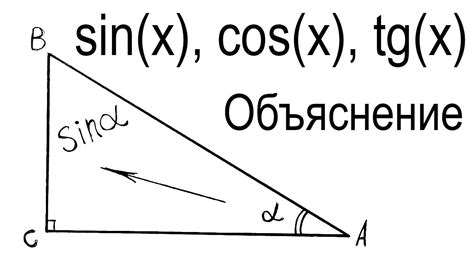
Синус широко используется в различных областях науки и техники, таких как физика, инженерия, астрономия и даже музыка. Он помогает в определении углов и расчете различных параметров внутри треугольника.
Формула для вычисления синуса угла равна отношению противолежащей стороны к гипотенузе:
- sin(угол) = противолежащая сторона / гипотенуза
Значение синуса всегда находится в диапазоне от -1 до 1, где -1 соответствует углу 270 градусов, а 1 соответствует углу 90 градусов.
Синус также имеет множество свойств и идентичностей, которые позволяют упростить вычисления и решение задач. Он используется в тригонометрических функциях, таких как косинус, тангенс и котангенс.



