Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны. Доказательство параллельности противоположных сторон является важной задачей геометрии. Если мы можем установить, что две противоположные стороны параллелограмма действительно параллельны, мы сможем использовать это свойство для решения других геометрических задач. В этой статье мы рассмотрим несколько способов доказательства параллельности противоположных сторон параллелограмма.
Первый способ основан на использовании свойств параллельных прямых. Если мы знаем, что два отрезка находятся на параллельных прямых, мы можем доказать, что эти отрезки также параллельны. Для доказательства параллельности противоположных сторон параллелограмма, воспользуемся этим фактом. Возьмем две противоположные стороны параллелограмма и проведем прямые, которыми они ограничены. Затем найдем точку пересечения этих прямых. Если точка пересечения лежит на третьей стороне параллелограмма, то стороны параллельны. В противном случае, стороны не являются параллельными.
Второй способ основан на использовании свойств углов параллельных прямых. Если мы знаем, что две прямые параллельны, мы можем доказать, что соответствующие углы на этих прямых равны. Применительно к параллелограмму, мы можем доказать параллельность противоположных сторон, основываясь на равенстве соответствующих углов. Для этого проведем дополнительные отрезки, которые соединяют концы противоположных сторон параллелограмма. Затем найдем соответствующие углы между этими отрезками. Если соответствующие углы равны, то стороны параллельны. В противном случае, стороны не являются параллельными.
Доказательство параллельности сторон параллелограмма

1. Доказательство с использованием диагоналей:
Рассмотрим параллелограмм ABCD. Пусть AC и BD - его диагонали.
а) Если диагонали AC и BD пересекаются в точке O и равны друг другу, то стороны AB и CD параллельны. Данное свойство следует из равенства треугольников ABO и CDO по стороне-углу-стороне.
б) Если диагонали AC и BD равны и точка их пересечения O является серединой каждой из них, то стороны AB и CD параллельны. Это следует из свойства параллелограмма, которое гласит, что диагонали параллелограмма делят его на два равных треугольника.
2. Доказательство с помощью соответствующих углов:
Если в параллелограмме ABCD угол A равен углу C и угол B равен углу D, то стороны AB и CD являются параллельными. Это следует из свойства параллелограмма, которое гласит, что противоположные углы равны.
Это лишь некоторые из возможных способов доказательства параллельности сторон параллелограмма. В каждом конкретном случае выбор метода доказательства зависит от условий задачи и доступных нам свойств данной фигуры.
Метод 1: Использование свойств параллелограмма
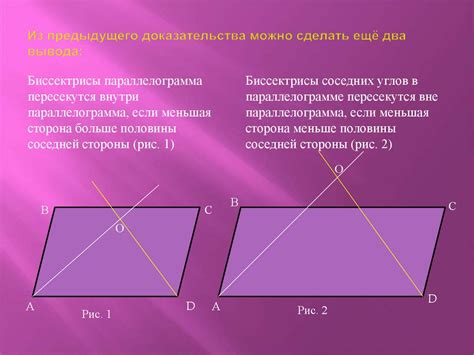
Для доказательства параллельности противоположных сторон параллелограмма можно использовать следующие свойства этой фигуры:
- Стороны параллелограмма являются противоположными и равными. Если стороны параллелограмма являются равными, то они также параллельны друг другу.
- Противоположные углы параллелограмма равны. Если углы параллелограмма равны, то противоположные стороны также параллельны.
- Диагонали параллелограмма делятся пополам. Если диагонали параллелограмма делятся пополам, то противоположные стороны также параллельны.
Метод 2: Отношение длин сторон параллелограмма
Другой способ доказательства параллельности противоположных сторон параллелограмма основан на использовании отношения длин этих сторон.
Давайте рассмотрим пример:
Пусть у нас есть параллелограмм ABCD, где AB = 6 см и BC = 3 см. Нам нужно доказать, что AD и DC параллельны.
Мы можем использовать отношение длин сторон, чтобы это сделать:
AB/BC = AD/DC
6/3 = AD/DC
2 = AD/DC
Мы видим, что отношение длин сторон AD и DC также равно 2, что подтверждает их параллельность.



