Ромб – это специальный вид параллелограмма, у которого все четыре стороны равны. Это особая геометрическая фигура, которая обладает рядом уникальных свойств и характеристик. В этой статье мы рассмотрим все основные свойства ромба и как они связаны между собой.
Одно из главных свойств ромба – это равенство всех его сторон. Все четыре стороны ромба имеют одинаковую длину, что делает его особенным среди других геометрических фигур. Благодаря равным сторонам, ромб обладает особыми свойствами и удобен для решения различных геометрических задач.
Другим важным свойством ромба является равенство его диагоналей. Диагонали ромба делят его на две равные треугольные части, и они имеют одинаковую длину. Также, в связи с равенством сторон и диагоналей, ромб является фигурой с осью симметрии. Любая прямая, проходящая через центр ромба, делит его на две равные части, что является еще одним важным свойством этой фигуры.
Ромб также обладает важным свойством органической геометрии – углы ромба смежных сторон суммируются до 360 градусов. Это означает, что сумма углов каждого треугольника ромба равна 180 градусам, и вся фигура состоит из четырех треугольников, сумма углов которых составляет 360 градусов. Это свойство позволяет легко рассчитать углы ромба при решении геометрических задач.
Ромб: определение и геометрические характеристики
У ромба есть несколько геометрических характеристик:
- Все стороны ромба равны друг другу. Это означает, что его диагонали тоже равны и перпендикулярны друг другу.
- Углы ромба являются прямыми. То есть, все углы ромба равны 90 градусам.
- Длина диагоналей ромба связана с длиной его сторон по формуле: диагональ_1 = √2 * сторона, диагональ_2 = √2 * сторона.
- Площадь ромба можно вычислить, зная длину его стороны или диагонали. Формула для вычисления площади: площадь = (диагональ_1 * диагональ_2) / 2.
- Периметр ромба можно вычислить, зная длину его стороны. Формула для вычисления периметра: периметр = 4 * сторона.
Ромб является основой для других геометрических фигур, таких как квадрат и ромбоид. Он также часто используется в архитектуре и дизайне.
Какой формы бывает ромб

Вертикальный ромб имеет две пары противоположных сторон, которые параллельны друг другу и перпендикулярны к горизонтальной оси. Горизонтальный ромб, напротив, имеет две пары противоположных сторон, которые параллельны горизонтальной оси и перпендикулярны к вертикальной оси.
Независимо от формы, ромб все равно остается ромбом, сохраняя свои основные свойства, такие как равенство всех сторон и смежных углов. Форма ромба влияет на его визуальное представление, что может быть полезно при решении различных геометрических задач.
Основные свойства ромба
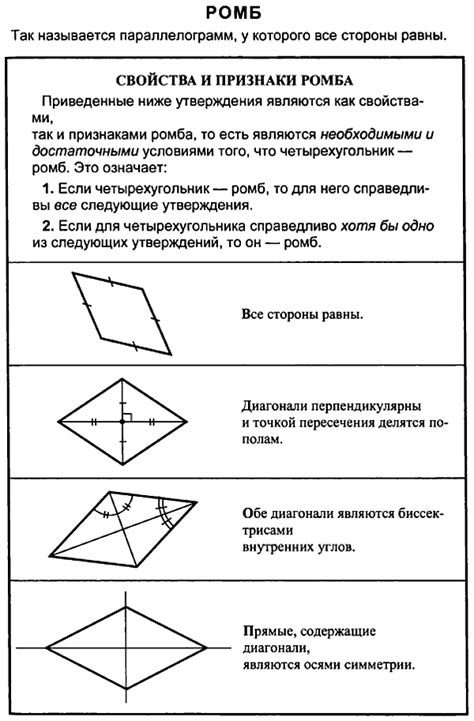
Кроме того, ромб обладает следующими характеристиками:
- Диагонали: Две диагонали ромба являются взаимно перпендикулярными и равны между собой. Диагонали делят ромб на четыре равных треугольника.
- Углы: Все углы ромба равны между собой. Угол ромба может быть любым, но сумма двух соседних углов всегда равна 180 градусов.
- Высоты: Ромб не имеет высоты, так как все его стороны и диагонали равны между собой.
- Периметр: Периметр ромба можно найти, сложив длины его четырех сторон.
- Площадь: Площадь ромба можно вычислить, умножив длину его диагоналей и разделив полученный результат на 2.
Эти основные свойства ромба являются ключевыми при решении задач на его конструкцию и вычисление различных параметров.
Стороны и углы в ромбе

В ромбе также все углы равны между собой. Каждый угол ромба составляет по 90 градусов, что делает его периметр равным четырем прямым углам.
Строка свойств ромба включает в себя следующие особенности:
- Все стороны ромба равны между собой.
- Все углы ромба равны между собой и составляют 90 градусов.
- Диагонали ромба перпендикулярны друг другу. Это значит, что они пересекаются под прямым углом.
- Длина каждой диагонали ромба равна половине суммы длин всех четырех его сторон.
Стороны и углы в ромбе обладают интересными свойствами, которые можно использовать для решения различных задач в математике и геометрии.
Диагонали ромба
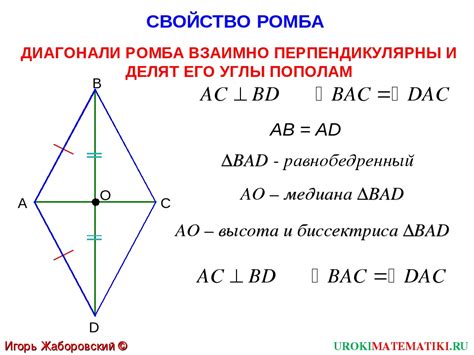
Диагонали ромба имеют несколько важных свойств:
- Диагонали ромба равны по длине. Это означает, что отрезок, соединяющий противоположные вершины ромба, имеет одинаковую длину. Можно обозначить диагонали как d1 и d2.
- Диагонали ромба перпендикулярны друг другу. Это означает, что диагонали образуют прямой угол на их точке пересечения.
- Диагонали ромба делятся на две равные части. Это означает, что отрезок каждой диагонали, соединяющий ее конечную точку с точкой пересечения диагоналей, делится пополам.
Диагонали ромба являются важным свойством этой фигуры и позволяют решать различные задачи и находить другие свойства ромба.
Сходство и различия ромба и квадрата

Основное сходство ромба и квадрата заключается в том, что обе фигуры являются параллелограммами. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине.
С другой стороны, ромб и квадрат имеют ряд отличий. Основное отличие заключается в своей форме. Ромб имеет четыре стороны равной длины, при этом углы ромба могут быть различными. Квадрат же является ромбом со всеми углами прямыми (90 градусов) и со всеми сторонами равной длины.
Еще одно отличие ромба от квадрата заключается в том, что ромб может иметь диагонали разной длины, в то время как у квадрата диагонали всегда равны и перпендикулярны друг другу.
Однако, ромб и квадрат также имеют общие свойства. Оба этих параллелограмма являются фигурами с равными противоположными углами и с двумя симметриями относительно центра фигуры и осей симметрии.
| Свойство | Ромб | Квадрат |
|---|---|---|
| Стороны | Равны по длине | Равны по длине |
| Углы | Могут быть различными | Все прямые (90 градусов) |
| Диагонали | Могут иметь разные длины | Равны по длине и перпендикулярны друг другу |
| Симметрия | Есть | Есть |
Площадь ромба
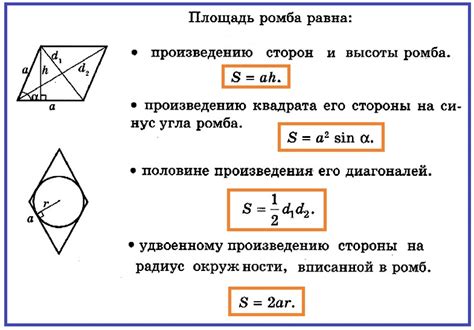
Если известны длины диагоналей ромба, то площадь можно вычислить, умножив их длины и разделив на 2:
Площадь = (диагональ_1 * диагональ_2) / 2
Если известны длина основания и высота ромба, то площадь можно найти, умножив длину основания на высоту и разделив результат на 2:
Площадь = (длина_основания * высота) / 2
Знание площади ромба может быть полезным при решении задач в геометрии или в повседневной практике, например, при расчете площади участка земли в форме ромба.
Формулы для вычисления периметра ромба
Периметр ромба можно вычислить несколькими способами, в зависимости от известных параметров.
1. Если известны все стороны ромба, то периметр можно вычислить, просуммировав их длины. Пусть сторона ромба равна a, тогда периметр будет равен P = 4a.
2. Если известна диагональ ромба, то периметр можно вычислить, умножив длину диагонали на коэффициент k. Коэффициент зависит от отношения длин диагоналей ромба. Пусть длина диагонали равна d, тогда периметр будет равен P = kd.
3. Если известны желаемые углы ромба, то периметр может быть вычислен по формуле P = 4a, где a - длина стороны ромба, определяемая углами. Длина стороны вычисляется по формуле a = \sqrt{2d_1d_2 \cdot \cos \alpha}, где d_1 и d_2 - длины диагоналей ромба, а \alpha - желаемый угол.
Используя эти формулы, вы можете легко вычислить периметр ромба, зная известные параметры.



