Перпендикуляр - это особый вид линии, который имеет огромное значение в математике. Перпендикуляр - это линия, которая пересекает другую линию или отрезок под прямым углом. Термин "перпендикуляр" происходит от латинского слова "perpendicularis", что означает "сходящийся наложением отдельных частей".
Понимание понятия "перпендикуляр" в 6 классе имеет фундаментальное значение, так как оно позволяет разобраться во многих математических задачах и решениях. Перпендикулярные линии или отрезки играют важную роль в геометрии и алгебре, а также находят применение в реальном мире, например, в строительстве и дизайне.
Знание перпендикуляра позволяет детям понимать геометрические понятия, такие как прямые углы, между которыми они образуются, и методы их измерения и пространственного расположения. Например, если две линии пересекаются, образуя прямой угол, то они являются перпендикулярными. Также знание перпендикуляров позволяет детям решать геометрические задачи, связанные с построением и измерением различных фигур.
В чем заключается значение перпендикуляра в математике для 6 класса?

Значение перпендикуляра заключается в том, что он позволяет определить направление и положение линий и отрезков относительно друг друга. Важно уметь строить перпендикулярные линии и откладывать расстояния по этим линиям, чтобы решать геометрические задачи и находить решения в других математических задачах.
Понимание перпендикуляра также помогает ученикам освоить концепцию прямых углов и различать их от острых и тупых углов. Перпендикулярная линия всегда образует прямой угол с другой линией, что может быть использовано при измерении углов и решении задач на построение.
Знание перпендикуляра также важно при изучении алгебры и координатной плоскости. Перпендикулярные линии имеют специальные свойства, которые могут помочь в построении графиков функций и решении уравнений.
Таким образом, понимание значения перпендикуляра позволяет ученикам развивать свои навыки геометрии и алгебры, а также использовать их для решения практических задач в математике и других науках.
Определение понятия "перпендикуляр" в математике

Перпендикуляр можно представить как две линии, которые пересекаются друг с другом, образуя прямой угол. Как правило, перпендикуляр обозначается символом ⊥. Чтобы визуально определить, что две линии или отрезка перпендикулярны друг другу, можно использовать специальный знак ⊥, который располагается перпендикулярно одной из линий.
На практике, понятие перпендикуляра используется для измерения углов, построения прямых, определения расстояния между объектами и многое другое. Формальное определение перпендикуляра включает также понятие ортогональности, то есть отсутствие взаимного пересечения линий.
Знание и понимание понятия "перпендикуляр" в математике позволяет решать геометрические задачи, строить планировки, а также применять полученные знания в реальной жизни, например, при построении зданий, дорог и других инженерных сооружений.
Специальные свойства перпендикуляра

- Перпендикулярные прямые никогда не пересекаются.
- Угол между перпендикулярными прямыми равен 90 градусам.
- Если две прямые пересекаются и образуют прямой угол, то они являются перпендикулярными.
- Любая прямая, перпендикулярная к одной из пересекающихся прямых, также является перпендикулярной к другой.
Перпендикуляр – важное понятие в геометрии. Оно используется для решения задач, связанных с построением перпендикуляров, определением наклонов и вычислением углов. Перпендикуляры также активно применяются в архитектуре, инженерии и других областях.
Примеры использования перпендикуляра в повседневной жизни

1. Построение зданий и строительство.
Перпендикуляр используется в строительстве для создания прямых и перпендикулярных углов при расстановке фундамента, стен и других строительных элементов. Он помогает определить вертикальное и горизонтальное положение структур, обеспечивая их устойчивость и правильную геометрию.
2. Школьные уроки и измерения.
Перпендикуляр используется в школьных учебниках и уроках геометрии для различных задач. Например, он помогает определить, как получить прямой угол при использовании чертежных инструментов, таких как линейка и угольник. Также перпендикуляр используется для измерения высоты зданий и деревьев, используя триангуляцию и методы подобия фигур.
3. Навигация и ориентирование.
Перпендикуляр также может использоваться для ориентирования в пространстве. Например, в картографии перпендикуляр используется для определения направления и создания сетки координат, что помогает нам находиться на определенном месте и следовать заданному пути.
4. Архитектура и дизайн.
Перпендикуляр используется в архитектуре и дизайне для создания симметричных и пропорциональных структур. Он помогает в создании правильных углов и линий, которые добавляют стабильность и красоту в здания, мебель и предметы искусства.
В заключении, перпендикуляр имеет широкое применение в повседневной жизни, начиная от строительства до дизайна. Понимание и использование этого понятия помогает нам создавать стабильные и гармоничные структуры вокруг нас.
Задачи с поиском перпендикуляра на плоскости

1. Задача: Найти перпендикуляр к прямой с заданными координатами точек.
Решение: Для решения этой задачи можно использовать формулу перпендикуляра, которая гласит, что если у прямой с координатами точек A(x1, y1) и B(x2, y2) коэффициент наклона равен k, то коэффициент наклона перпендикуляра будет равен -1/k. Таким образом, мы можем найти уравнение перпендикуляра и использовать его для нахождения нужной прямой.
2. Задача: Найти перпендикуляр, опущенный из точки на прямую.
Решение: Для решения этой задачи нужно найти уравнение прямой и использовать формулу перпендикуляра, описанную выше. Найденное уравнение перпендикуляра будет проходить через данную точку и быть перпендикулярным к данной прямой.
3. Задача: Найти перпендикуляр, проходящий через середину отрезка.
Решение: Для решения этой задачи нужно найти координаты середины отрезка и использовать формулу перпендикуляра. Если уравнение прямой, проходящей через середину отрезка, равно y = mx + b, то уравнение перпендикуляра будет иметь вид y = -1/mx + b', где b' - новый коэффициент "b".
| Задача | Решение |
|---|---|
| 1. Найти перпендикуляр к прямой с координатами А(1, 2) и B(3, 4). | Используя формулу перпендикуляра, находим коэффициент наклона перпендикуляра: k = -1/((4-2)/(3-1)) = -1/1 = -1. Уравнение прямой, проходящей через точку A(1, 2) и имеющей коэффициент наклона -1, имеет вид y = -x + b. Подставляем координаты точки A в уравнение прямой и находим b = 3. Таким образом, уравнение перпендикуляра будет иметь вид y = x + 3. |
| 2. Найти перпендикуляр, опущенный из точки A(2, 5) на прямую с уравнением y = 2x - 1. | Используя формулу перпендикуляра, находим коэффициент наклона перпендикуляра: k = -1/2. Уравнение прямой, проходящей через точку A(2, 5) и имеющей коэффициент наклона -1/2, будет иметь вид y = (-1/2)x + b. Подставляем координаты точки A в уравнение прямой и находим b = 6. Таким образом, уравнение перпендикуляра будет иметь вид y = (1/2)x + 6. |
| 3. Найти перпендикуляр, проходящий через середину отрезка с конечными точками A(1, 3) и B(5, 7). | Найдем координаты середины отрезка: x = (1+5)/2 = 3, y = (3+7)/2 = 5. Используя формулу перпендикуляра, находим коэффициент наклона перпендикуляра: k = -1/((7-3)/(5-1)) = -1/1 = -1. Уравнение прямой, проходящей через точку (3, 5) и имеющей коэффициент наклона -1, будет иметь вид y = -x + b. Подставляем координаты точки (3, 5) в уравнение прямой и находим b = 8. Таким образом, уравнение перпендикуляра будет иметь вид y = x + 8. |
Как строить перпендикуляр с помощью циркуля и линейки
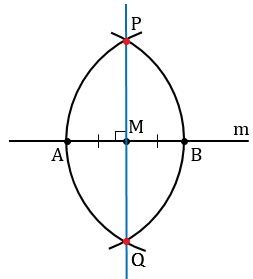
Для построения перпендикуляра с помощью циркуля и линейки следуйте следующим шагам:
- Возьмите линейку и нарисуйте отрезок, который будет служить основой для перпендикуляра.
- Установите циркуль на одном из концов отрезка и нарисуйте дугу, пересекающую оба конца отрезка.
- Не меняя радиуса циркуля, установите его на втором конце отрезка и нарисуйте еще одну дугу так, чтобы она пересекала первую дугу.
- Соедините точки пересечения дуг прямой линией с помощью линейки.
Таким образом, вы построили перпендикуляр к данному отрезку с помощью циркуля и линейки.
Практическое применение перпендикуляра в архитектуре и строительстве

Архитектура и строительство – области, где точность и правильность измерений имеют огромное значение. Использование перпендикуляра в этих областях позволяет точно и правильно измерять и строить здания, создавая качественную и надежную конструкцию.
Одним из примеров практического применения перпендикуляра является использование его для построения прямых углов. Перпендикулярная линия, проведенная от одной точки к другой, создает угол в 90 градусов. Использование прямых углов в архитектуре и строительстве позволяет создавать максимально прочные и стабильные конструкции.
Также перпендикуляр используется для построения перпендикулярных стен, оснований и фундаментов. Правильное применение перпендикуляра в строительстве обеспечивает равномерное распределение веса и нагрузок, предотвращая возможные деформации и повреждения конструкции.
| Применение перпендикуляра | Описание |
|---|---|
| Построение прямых углов | Создание устойчивых и прочных конструкций |
| Построение перпендикулярных стен, оснований и фундаментов | Обеспечение равномерного распределения нагрузок и предотвращение деформаций |
Использование перпендикуляра в архитектуре и строительстве способствует созданию безопасных и устойчивых сооружений. Он позволяет контролировать и поддерживать геометрическую точность при проектировании и строительстве зданий и сооружений.
Таким образом, понимание и умение работать с понятием перпендикуляра в математике имеет огромное практическое значение в архитектуре и строительстве. Оно позволяет создавать надежные конструкции и обеспечивать безопасность в данной области.



