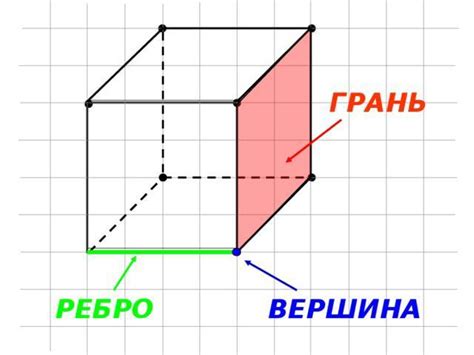
Многогранные фигуры - удивительные объекты, которые встречаются в различных сферах нашей жизни. Они имеют множество особенностей, и одной из важных характеристик многогранника является его грань. Грань - это плоская поверхность, ограниченная ребрами. Ребро - это отрезок, соединяющий две вершины многогранника.
Однако, в многогранных фигурах, у которых есть диагональ, ребра грани могут стать диагоналями вершин. Диагональ - это отрезок, соединяющий две вершины многогранника, которые не являются соседними.
Таким образом, ребра грани диагонали вершины многогранника - это ребра, которые лежат в грани и являются диагоналями вершин. Они позволяют установить связь между вершинами, которые не соседствуют друг с другом, и внести асимметрию в структуру многогранника.
Часть 1: Определение многогранника и его вершины
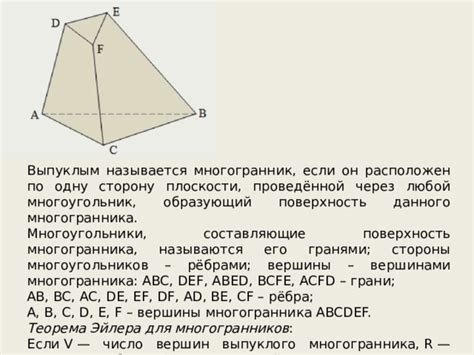
Вершины многогранника могут быть угловыми или нет. Угловые вершины - это вершины, в которых сходятся три или более ребра. Неугловые вершины - это вершины, в которых сходятся два ребра. Все вершины многогранника связаны ребрами, которые являются прямыми отрезками между вершинами.
Ребра грани диагонали вершины многогранника - это ребра, которые соединяют две вершины, не принадлежащие одной грани. Они пересекают грани многогранника и могут иметь различные длины и углы наклона в зависимости от формы и структуры многогранника.
Часть 2: Понятие грани многогранника

Грань многогранника - это плоская фигура, ограниченная ребрами. Грани многогранника могут быть различных форм и размеров, но они всегда плоские. Грани характеризуются своей формой, количеством ребер и углами, которые образуются между ребрами.
Каждая грань многогранника имеет свое название в зависимости от количества ребер, которые ее образуют:
- Грань с тремя ребрами называется треугольником.
- Грань с четырьмя ребрами называется четырехугольником или квадратом.
- Грань с пятью ребрами называется пятиугольником или пентагоном.
Также грани многогранника могут быть большей сложности. Например, если грань имеет шесть ребер, то она называется шестиугольником или гексагоном.
Каждая грань имеет свои ребра, которые образуют ее края. Грани многогранника могут быть прямоугольными, треугольными, многоугольными или неправильной формы. Зная количество ребер, образующих грань, мы можем определить, какая это грань и как она выглядит.
Грани многогранника важны для его классификации и изучения его свойств. Они помогают нам понять структуру многогранника и его форму. Изучение граней многогранника позволяет нам определить, какие тела можно назвать многогранниками, а какие нет.
Часть 3: Ребра многогранника и их роль
Ребра многогранника определяются как отрезки, соединяющие вершины многогранника. Они играют важную роль в определении геометрии и свойств многогранника. Ребра формируют грани многогранника, являясь их сторонами и границами.
Ребра грани многогранника выполняют несколько функций. Во-первых, они определяют форму и структуру грани, влияя на ее внешний вид. Размер и форма ребер могут быть различными, что позволяет граням многогранника иметь разнообразные формы и контуры.
Во-вторых, ребра служат для определения взаимного расположения граней. Пересечение ребер граней указывает на то, что эти грани связаны между собой и имеют общие вершины. Ребра также определяют, какие грани являются смежными, то есть имеют общие ребра и вершины.
Третья роль ребер заключается в определении свойств многогранника. Например, длины ребер могут использоваться для вычисления площади грани или объема многогранника. Кроме того, связь между ребрами и вершинами позволяет определить углы между гранями и другими характеристики многогранника.
Исследование ребер многогранника помогает понять его структуру и свойства. Анализируя ребра грани диагонали вершины многогранника, можно выявить особенности и взаимосвязи различных элементов многогранника, что способствует более глубокому пониманию геометрической природы этого объекта.
Часть 4: Понятие диагонали многогранника
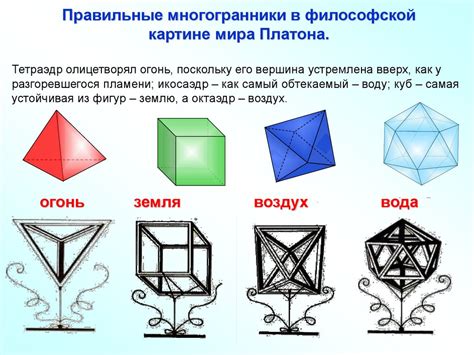
Диагонали многогранника имеют большое значение при изучении его свойств и характеристик. Они позволяют определить степень сложности многогранника, а также выявить его особенности и уникальные свойства.
Для того чтобы лучше представить себе диагонали многогранника, можно рассмотреть примеры диагоналей в различных многогранниках:
| Многогранник | Пример диагоналей |
|---|---|
| Тетраэдр | Диагонали могут быть любыми ребрами, соединяющими несоседние вершины. |
| Куб | В кубе каждая диагональ соединяет противоположные вершины. |
| Октаэдр | Диагонали могут быть ребрами или диагоналями вершин на каждой грани. |
Диагонали многогранника позволяют установить связи между его вершинами, гранями и ребрами. Они способствуют более глубокому пониманию структуры и формы многогранника, а также помогают решать задачи, связанные с его анализом и исследованием.
Часть 5: Ребра грани и их взаимосвязь
Ребра грани могут быть связаны друг с другом и образовывать специальные структуры. Например, два ребра грани называются смежными, если они имеют общую вершину. Таким образом, каждое ребро грани смежно с двумя другими ребрами грани, если грань не является краевой. Для краевой грани каждое ребро смежно только с одним ребром грани.
Также ребра грани могут быть параллельными друг другу или пересекаться. Два ребра грани называются параллельными, если они лежат в одной плоскости и не пересекаются. В противном случае, если ребра пересекаются, они называются непараллельными.
Ребра грани также могут быть прямолинейными или изогнутыми. Прямолинейные ребра образуются из отрезков, а изогнутые ребра имеют кривую форму. Форма ребер грани зависит от формы самой грани и особенностей многогранника.
Ребра грани являются важными элементами многогранника и определяют его форму и структуру. Ребра грани могут быть смежными или не смежными, параллельными или непараллельными, прямолинейными или изогнутыми. Понимание взаимосвязи ребер грани позволяет более глубоко изучить свойства и особенности многогранника.
Часть 6: Роль вершины в формировании ребер грани
Рассмотрим пример. Представим многогранник с пятью вершинами, обозначенными как A, B, C, D и E. Если мы возьмем две любые вершины и соединим их ребром, мы получим одно из ребер грани многогранника. Например, ребро AB связывает вершины A и B, ребро BC связывает вершины B и C, и так далее.
Таким образом, для формирования каждого ребра грани многогранника необходимо выбрать две вершины и соединить их. Это позволяет определить грани многогранника и дает ему определенную форму и структуру.
Ребра грани являются важными элементами для изучения свойств многогранников и позволяют нам анализировать их форму, размеры и соотношения между сторонами. Кроме того, понимание роли вершин в формировании ребер грани помогает нам лучше понять структуру многогранников и их свойства.
В данной статье мы рассмотрели основные понятия, связанные с ребрами грани диагонали вершины многогранника. Важно понимать, что ребра грани диагонали вершины играют ключевую роль в определении структуры и свойств многогранника.
Ребра грани диагонали вершины многогранника представляют собой отрезки, соединяющие вершины грани и позволяющие определить ее форму и размеры. Количество ребер грани диагонали вершины может варьироваться в зависимости от типа многогранника.
Понимание ребер грани диагонали вершины многогранника позволяет анализировать его структуру и свойства. Например, знание количества ребер грани диагонали вершины может помочь определить число граней и вершин многогранника. Кроме того, ребра грани диагонали вершины многогранника могут быть использованы для вычисления его объема, площади и других характеристик.
Также, понимание ребер грани диагонали вершины многогранника является важным для работы с пространственными моделями и различными приложениями, связанными с геометрией и графикой. Знание структуры и свойств многогранника помогает создавать более эффективные и точные модели, а также улучшает представление данных и их визуализацию.
В итоге, понимание ребер грани диагонали вершины многогранника имеет большое значение в геометрии и вычислительной геометрии. Это необходимо для работы с многогранниками и их анализа, а также для создания более точных и эффективных моделей и приложений.



