В мире математики существуют разряды и классы чисел, которые отражают их особенности и свойства. Разряды чисел определяют их различные порядки и положение в числовой системе. Классы чисел, в свою очередь, группируют числа по их общим характеристикам и свойствам.
Разряды чисел являются основой для понимания структуры числовой системы. Каждая позиция числа в числовой записи имеет свой разряд, который задает его значение. Например, в десятичной системе счисления первый разряд отражает количество единиц, второй разряд - количество десятков, третий - количество сотен и так далее. Переход от одного разряда к другому связан с умножением или делением числа на основу системы счисления.
Классы чисел группируют числа по общим свойствам и характеристикам. Они позволяют нам описывать и анализировать числа в контексте их специфических свойств. Некоторые из классов чисел включают натуральные числа, целые числа, рациональные числа, иррациональные числа, действительные числа и комплексные числа. Каждый класс имеет свои особенности и интересные свойства, которые могут быть использованы для решения различных математических задач.
Разряды чисел - что это такое и почему важно разбираться
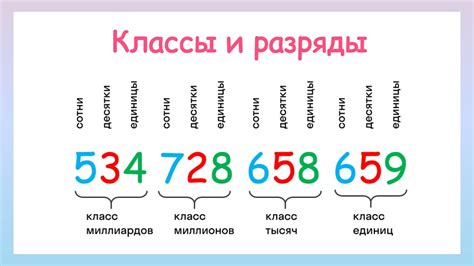
Понимание разрядов чисел имеет важное значение в математике и ряде других областей. Во-первых, разряды чисел помогают нам читать и записывать числа правильно. Например, в числе 327, цифра "7" находится в разряде единиц, цифра "2" - в разряде десятков, а цифра "3" - в разряде сотен. Это позволяет нам точно интерпретировать число и понимать его размер.
Кроме того, понимание разрядов чисел необходимо для выполнения математических операций, таких как сложение, вычитание, умножение и деление. Когда мы складываем или вычитаем числа, мы работаем с разрядами, чтобы правильно сгруппировать и сложить или вычесть цифры. Важно понимать, какие разряды участвуют в операции, чтобы получить правильный результат.
Особое значение разрядов чисел имеет в ряде научных и технических областей. Например, в компьютерной науке, понимание разрядности чисел (например, разрядности байта или бита) является критическим для хранения и обработки данных. Точное представление и обработка чисел с помощью правильной разрядности является основой для многих алгоритмов и приложений.
Число и его структура
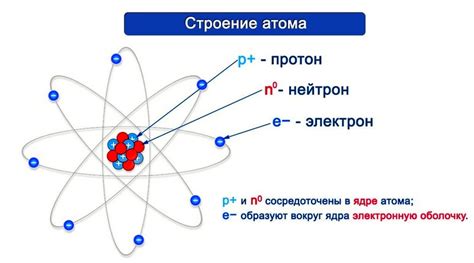
Число в математике представляет собой абстрактное понятие, которое используется для измерения количества или порядка объектов. Однако число само по себе имеет определенную внутреннюю структуру, которая определяет его разряды и классы.
Разряды числа – это его составные части, которые указывают на количество мест перед и после десятичной точки. Каждый разряд имеет свое значение, которое зависит от его позиции. Наиболее распространенная система разрядов – это десятичная система с базой 10, где каждый разряд увеличивается в 10 раз по сравнению с предыдущим.
Классы чисел также определяются его структурой и влияют на его понимание и использование. Существуют различные классы чисел, такие как натуральные числа, целые числа, рациональные числа и иррациональные числа. Натуральные числа – это положительные целые числа, которые используются для подсчета объектов. Целые числа включают в себя натуральные числа и их отрицательные значения. Рациональные числа – это числа, которые могут быть представлены в виде дроби p/q, где p и q – целые числа, а q не равно нулю. Иррациональные числа не могут быть представлены в виде дроби и имеют бесконечную десятичную дробь без периода.
Понимание структуры числа позволяет проводить операции над числами более точно и эффективно. Знание разрядов и классов чисел помогает в решении математических задач, использовании чисел в реальных ситуациях и дальнейшем изучении более сложных математических концепций.
Разряды чисел - основные понятия
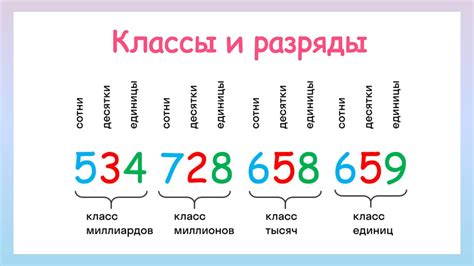
В десятичной системе счисления числа состоят из десяти разрядов, начиная с единицы и заканчивая девятками. Первый (самый правый) разряд числа называется единицами, второй - десятками, третий - сотнями, и так далее. Левая сторона числа отделяется запятой и состоит из разрядов, которые увеличиваются в разы. Пример: в числе 123,45 единицей является цифра 3, десятками - цифра 2, сотнями - цифра 1, тысячами - цифра 0 и т. д.
Каждый разряд числа имеет свою весовую значимость. Например, в десятичной системе счисления весовые значимости разрядов увеличиваются в 10 раз справа налево: единицы имеют вес 1, десятки - вес 10, сотни - вес 100 и так далее. Таким образом, число 123,45 можно разложить на сумму произведений каждой цифры на ее весовую значимость: 3 * 1 + 2 * 10 + 1 * 100 + 4 * 0.1 + 5 * 0.01.
Разряды чисел важны при выполнении арифметических операций, таких как сложение, вычитание, умножение и деление. Правильное определение разрядов помогает выполнить операции с числами корректно и получить правильный результат.
Знание основных понятий и свойств разрядов чисел является фундаментом для понимания и работы с числами в математике и других областях, где требуется использование числовых данных.
Важно: при работе с разрядами чисел необходимо быть внимательным и точным, чтобы избежать ошибок и получить правильные результаты вычислений.
Классы чисел и их значение
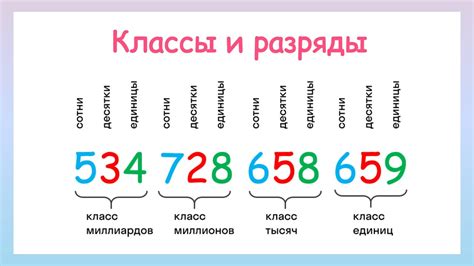
В математике числа разделяются на различные классы в зависимости от их свойств и характеристик. Классификация чисел позволяет систематизировать их и описать особенности каждого класса.
Одним из основных классов чисел являются натуральные числа. Они представляют собой положительные целые числа, начиная с единицы и не имеющие ограничений сверху. Натуральные числа используются для обозначения количества объектов, расположения в порядке и т.д. Они также играют важную роль в алгебре, геометрии и других разделах математики.
Целые числа - это класс чисел, включающий все натуральные числа, их противоположности (отрицательные числа) и ноль. Целые числа используются для описания задолженностей, температуры, глубины и других значений, которые могут быть как положительными, так и отрицательными.
Рациональные числа - это числа, представимые в виде обыкновенных дробей (отношений двух целых чисел), а также десятичных дробей или конечных и периодических десятичных дробей. Они включают в себя все целые числа, натуральные числа и десятичные числа. Рациональные числа широко используются в научных расчетах и инженерии.
Но рациональные числа не могут покрыть все числовое пространство. Это приводит нас к классу чисел, называемому иррациональными числами. Иррациональные числа не могут быть представлены в виде обыкновенных дробей и имеют бесконечное число недолгих десятичных знаков. Примерами иррациональных чисел являются число π (пи) и корень из двух.
Примечательно, что рациональные и иррациональные числа вместе образуют класс действительных чисел. Действительные числа включают в себя все рациональные и иррациональные числа и широко используются в физике, экономике и других науках.
Классы чисел играют важную роль в алгебре, анализе и других математических дисциплинах. Они позволяют нам обозначать, сравнивать и оперировать числами согласно их специфическим свойствам и потенциальному применению.
Значение разрядов при работе с большими числами
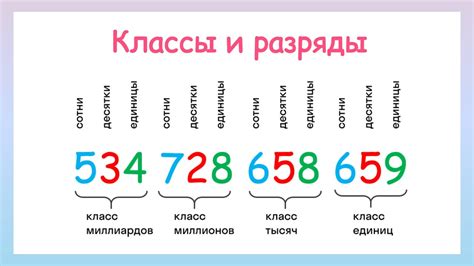
Разряды играют важную роль при работе с большими числами. Каждая цифра в числе занимает свое место, определенное разрядом. Разряды определяют вес и значение цифр, а также позволяют представить числа в удобной и компактной форме.
Система разрядов основывается на 10-тичной системе счисления. В числе каждая цифра занимает свое место, которое определяется степенью числа 10. Например, в числе 123, цифра 3 находится в единичном разряде, цифра 2 - в десятичном разряде, а цифра 1 - в сотенном разряде.
Разряды значимости цифр в числе увеличиваются справа налево. Наименьший разряд называется единичным или нулевым разрядом, и он имеет наименьший вес. Затем следуют десятичный разряд, сотенный разряд, тысячный разряд и так далее. Чем правее цифра расположена, тем меньший вес она имеет.
Значение разряда определяется путем умножения цифры на ее вес. Например, в числе 123, цифра 3 в единичном разряде имеет значение 3, цифра 2 в десятичном разряде имеет значение 20, а цифра 1 в сотенном разряде имеет значение 100.
| Разряд | Значение | Пример |
|---|---|---|
| Единичный | 10^0 | 3 (в числе 123) |
| Десятичный | 10^1 | 20 (в числе 123) |
| Сотенный | 10^2 | 100 (в числе 123) |
| Тысячный | 10^3 | 1000 (в числе 1234) |
Использование разрядов позволяет оперировать и представлять большие числа более эффективно. Кроме того, знание разрядов позволяет легче разбираться в структуре числа и производить различные операции с ним.
Роль разрядов в программировании и вычислениях

Разряды числа играют важную роль в программировании и вычислениях. Каждый разряд представляет определенную степень числа, которая определяет его величину и вес. Например, в десятичной системе счисления число 356 имеет разряды с весами 100, 10 и 1.
В программировании разряды используются для хранения и обработки чисел. Целые числа часто представляются в битовом представлении, где каждый бит является разрядом. Например, в двоичной системе счисления число 1011 имеет разряды с весами 8, 4, 2 и 1.
Разряды также используются при выполнении арифметических операций. При сложении или вычитании двух чисел разряды складываются или вычитаются в соответствующих позициях. Например, при сложении чисел 235 и 172, разряды единиц складываются (5 + 2 = 7), разряды десятков складываются (3 + 7 = 10), и разряды сотен складываются (2 + 1 = 3).
Разряды также важны при выполнении операций с плавающей точкой. Для представления чисел с плавающей точкой используется система счисления, основанная на разрядах. Разряды указывают на положение точки и определяют точность представления числа.
Понимание роли разрядов в программировании и вычислениях необходимо для эффективного решения задач, связанных с числами. Знание разрядов помогает понять, как числа представляются и обрабатываются в компьютере, что является основой для разработки эффективных алгоритмов и программ.



