Размеры объектов играют важную роль при проектировании и строительстве. Квадраты могут быть одной из самых простых геометрических фигур, но вычисление размера и измерение диагонали квадрата, особенно когда речь идет о больших объектах, может вызывать определенные сложности.
Вычисление диагонали квадрата дает нам информацию о расстоянии между двумя противоположными углами, задает параметры для укладки плитки, обустройства пола или других строительных работ. Диагональ позволяет определить точное расстояние и угол между двумя сторонами квадрата, а также его диагонали, что является важным фактором во многих практических задачах.
Измерение диагонали квадрата 3 метра на 3 метра может быть произведено с простыми инструментами, такими как линейка, измерительная лента или уровень. Чтобы вычислить диагональ, нужно знать формулу, используемую для нахождения длины гипотенузы в треугольнике, где оба катета равны 3 метра.
Как вычислить и измерить размер диагонали квадрата 3м на 3м
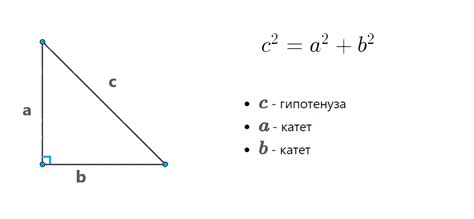
Диагональ квадрата можно вычислить с использованием теоремы Пифагора. Для квадрата со стороной 3м, длина диагонали можно определить следующим образом:
| Сторона квадрата | Длина диагонали |
|---|---|
| 3м | 3√2м |
Чтобы измерить диагональ квадрата, можно воспользоваться лентой или измерительной линейкой. Удобно начинать измерение от одного угла квадрата и проводить линию через противоположный угол. После чего считывается результат измерения на инструменте.
Таким образом, для квадрата со стороной 3м, длина его диагонали составит примерно 4.243м, согласно теореме Пифагора.
Что такое диагональ квадрата
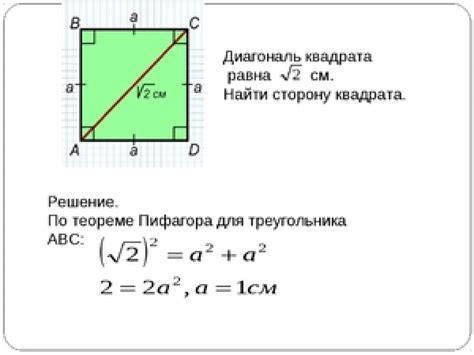
Чтобы вычислить длину диагонали квадрата, нужно знать длину его стороны, поскольку все стороны равны между собой. Для квадрата со стороной 3 метра, длина диагонали равна длине отрезка, соединяющего две противоположные вершины и проходящего через центр квадрата.
Для вычисления длины диагонали квадрата можно использовать теорему Пифагора. Если сторона квадрата равна a, то длина диагонали d вычисляется по формуле: d = a√2. Таким образом, для квадрата со стороной 3 метра, длина диагонали составит примерно 4,242 метра.
Чтобы измерить длину диагонали квадрата на практике, можно использовать сантиметр или ленту измерения. Положите один конец ленты на одну из противоположных вершин квадрата и протяните ее до другой противоположной вершины. Измерьте расстояние, получившееся на ленте, и это будет длина диагонали квадрата.
Зачем нужно вычислять и измерять размер диагонали
Вычисление и измерение размера диагонали квадрата 3м на 3м имеет свою важность и используется во многих сферах.
1. Расчет площади: Зная размеры диагонали квадрата и используя соответствующую формулу, можно вычислить его площадь. Это полезно в строительстве и архитектуре, так как позволяет определить стоимость материалов и планировать использование пространства.
2. Определение геометрических параметров: Размер диагонали квадрата является важным параметром при установке и выравнивании оборудования и мебели. Зная длину диагонали, можно точно определить требуемое расстояние и обеспечить правильное размещение предметов.
3. Измерение степени ровности поверхности: Вычисление диагонали квадрата позволяет определить, насколько ровной является поверхность. Если диагональ отличается от ожидаемого значения, это может указывать на неровности или деформации, которые могут потребовать корректировки или ремонта.
4. Решение геометрических задач: Измерение размера диагонали квадрата может понадобиться для решения различных геометрических задач. Например, для нахождения расстояния между двумя точками или вычисления углов.
Итак, вычисление и измерение размера диагонали квадрата 3м на 3м имеет практическую и теоретическую значимость, а также применяется в различных областях деятельности, связанных с геометрией и измерениями.
Как вычислить размер диагонали квадрата 3м на 3м
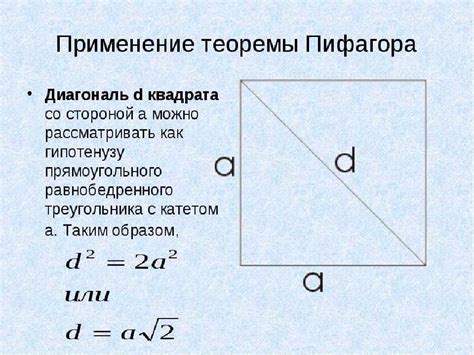
Вычисление размера диагонали квадрата 3м на 3м может показаться сложной задачей, но на самом деле это довольно просто.
Для начала, нужно помнить, что в квадрате все стороны равны друг другу и углы прямые.
Чтобы вычислить длину диагонали, можно воспользоваться теоремой Пифагора, которая устанавливает, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
В нашем случае, гипотенуза - это диагональ квадрата, а катеты - его стороны. Длина стороны квадрата составляет 3м, следовательно, квадрат катета будет равен 3^2 = 9.
Применяя теорему Пифагора, получим следующее уравнение: гипотенуза^2 = катет^2 + катет^2.
Подставим известные значения в уравнение: гипотенуза^2 = 9 + 9 = 18.
Чтобы найти длину диагонали, нужно извлечь квадратный корень из обеих сторон уравнения.
Итак, длина диагонали квадрата 3м на 3м составляет √18м, что можно упростить до примерно 4,24м (округленно).
Пример вычисления размера диагонали

Для вычисления размера диагонали квадрата нужно использовать теорему Пифагора. Эта теорема указывает на связь между сторонами прямоугольного треугольника.
В нашем случае, диагональ квадрата является гипотенузой прямоугольного треугольника, а две стороны квадрата являются катетами. Поэтому формула для вычисления размера диагонали будет выглядеть следующим образом:
диагональ = √(сторона^2 + сторона^2)
Если сторона квадрата равна 3 метрам, то подставляем это значение в формулу:
диагональ = √(3^2 + 3^2)
Выполняем вычисления:
диагональ = √(9 + 9) = √18 ≈ 4,242 метра
Таким образом, размер диагонали квадрата 3м на 3м составляет примерно 4,242 метра.
Как измерить размер диагонали квадрата 3м на 3м
Измерение размера диагонали квадрата 3м на 3м может быть выполнено с помощью простых математических вычислений и использования измерительной ленты. Для того чтобы измерить диагональ квадрата, следуйте следующим шагам:
- Возьмите измерительную ленту и разместите ее в одном из углов квадрата.
- Натяните измерительную ленту через диагональный угол квадрата, чтобы она проходила через противоположный угол.
- Зафиксируйте измерительную ленту на обоих концах диагонали с помощью скрепок или прищепок.
- Считайте число, указанное на измерительной ленте, и запишите его.
Таким образом, вы сможете узнать точное значение диагонали квадрата 3м на 3м. Не забудьте учитывать любые погрешности, которые могут возникнуть при измерении.



