Синус пи деленное на 2 – это одно из наиболее известных и широко используемых значений тригонометрической функции синус. Оно часто встречается в математических вычислениях, физических формулах и инженерных решениях. Именно значение синуса пи деленное на 2 занимает особое место в числовых таблицах и учебниках.
Значение синуса пи деленное на 2 равно 1. То есть, sin(π/2) = 1. Это следует из определения синуса как отношения противолежащего катета к гипотенузе в прямоугольном треугольнике.
В тригонометрии и математическом анализе синус является периодической функцией, график которой представляет собой волну, колеблющуюся между значениями -1 и 1. Значение синуса пи деленное на 2 является частным случаем, когда аргумент функции равен половине периода, и поэтому синус равен единице.
Знание значения синуса пи деленное на 2 часто используется в физических и математических расчетах, особенно для угловых измерений и преобразований. Это значение также широко применяется в компьютерной графике, робототехнике и других областях, где требуется точное описание углов и движений.
Значение синуса пи деленного на 2
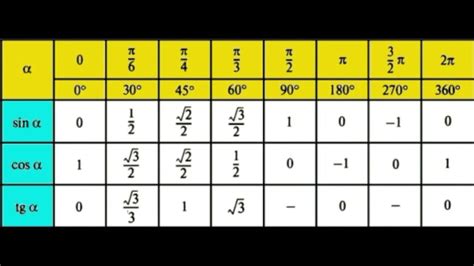
Значение синуса числа пи деленного на 2 равно 1.
Синус пи деленного на 2 может быть выражен следующей формулой: sin(pi/2) = 1.
Это означает, что при делении числа пи на 2 и нахождении синуса получается единичное значение. Синус пи/2 является одним из наиболее используемых и важных значений синуса, которое приходит на ум при решении тригонометрических уравнений и задач.
Также стоит отметить, что синус функция является периодической и имеет множество значений. Однако синус пи/2 всегда будет равен 1, независимо от того, в каком измерении угла вычисляется.
Способы расчета синуса пи деленного на 2
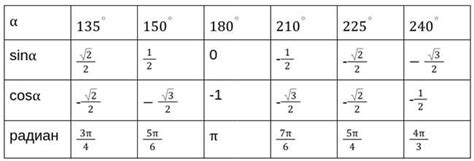
Существует несколько способов расчета этого значения. Один из них - использование свойств и тригонометрических формул. Согласно одному из этих свойств, sin(π/2) равен значению косинуса угла 0, так как синус и косинус являются сопряженными функциями. Таким образом, sin(π/2) = cos(0) = 1.
Другой способ - использование ряда Маклорена для функции синус. Согласно этому ряду, sin(x) можно представить в виде бесконечной суммы их слагаемых. Подставляя в этот ряд значение π/2, получаем sin(π/2) = π/2 - (π/2)^3/3! + (π/2)^5/5! - (π/2)^7/7! + ... = 1.
Кроме того, существуют различные методы численного расчета значения sin(π/2). Один из таких методов - использование аппроксимации тригонометрической функции через рациональные дроби. Примерно sin(π/2) можно приблизить значением 0.997, однако это приближение не является точным.
Независимо от выбранного способа расчета, значение синуса пи деленного на 2 всегда будет равно единице.



