В математике и геометрии существует множество интересных и важных задач, одной из которых является определение радиуса вписанного треугольника в окружность. Это вопрос, который волнует многих учеников и студентов, а также вызывает интерес у профессионалов в области математики.
Окружность, описанная вокруг треугольника, называется описанной окружностью, а окружность, вписанная в треугольник, называется вписанной окружностью. Радиус вписанной окружности имеет важное значение и может быть вычислен с использованием различных методов. Он является ключевым элементом при решении множества задач и определении свойств треугольника.
Существует несколько способов вычисления радиуса вписанного треугольника. Одним из самых известных и широко используемых методов является формула радиуса вписанной окружности, которая основана на понятии полупериметра треугольника. Полупериметр треугольника - это сумма длин его сторон, деленная на 2. Именно этот параметр играет важную роль при вычислении радиуса вписанной окружности.
Определение радиуса вписанного треугольника
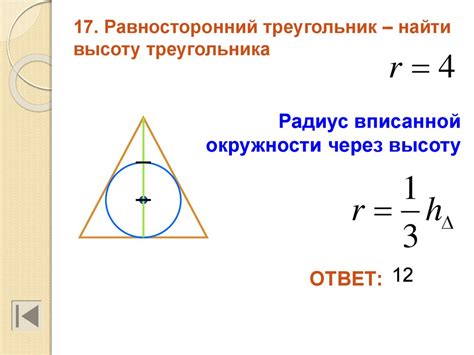
Для определения радиуса вписанного треугольника можно использовать формулу для вычисления площади треугольника. Зная площадь треугольника и длину одной из его сторон, можно найти радиус окружности с помощью следующей формулы:
Радиус = Площадь треугольника / Полупериметр треугольника
Полупериметр треугольника можно вычислить, сложив длины всех его сторон и разделив полученную сумму на 2.
Определение радиуса вписанного треугольника может быть полезно при решении различных геометрических задач, например, при определении площади треугольника или вычислении координат его вершин.
Что такое вписанный треугольник в окружность
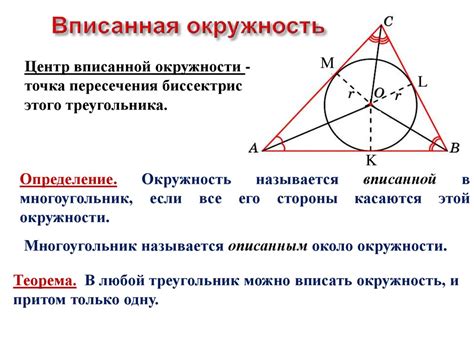
Самое важное свойство вписанного треугольника заключается в том, что сумма углов, образованных вершинами треугольника и центром окружности, равна 360 градусов. Это свойство является следствием определения вписанного угла – угла, стороны которого касаются окружности.
Другое важное свойство вписанного треугольника связано с его сторонами. Если провести высоту треугольника, начинающуюся в вершине и перпендикулярную соответствующей стороне, она всегда будет проходить через центр окружности. Соответственно, радиус окружности, в которую вписан треугольник, будет равен длине проведенной высоты.
Вписанный треугольник в окружность имеет много других интересных свойств, которые широко применяются в геометрии и ее приложениях. Изучение и использование этих свойств позволяет решать различные геометрические задачи и находить интересные закономерности в геометрических фигурах.
Как найти радиус вписанного треугольника
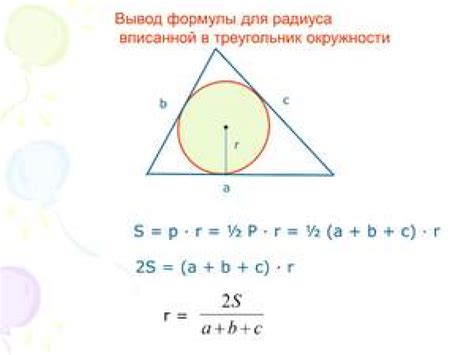
Существует несколько способов найти радиус вписанного треугольника:
1. Формула радиуса вписанной окружности:
Радиус вписанной окружности можно выразить через площадь треугольника и его полупериметр. Формула выглядит следующим образом:
R = S / p,
где R - радиус вписанной окружности, S - площадь треугольника, p - полупериметр треугольника.
2. Формула радиуса вписанной окружности через длины сторон треугольника:
Также существует формула, которая позволяет выразить радиус вписанной окружности через длины сторон треугольника:
R = (a * b * c) / (4 * S),
где R - радиус вписанной окружности, a, b, c - длины сторон треугольника, S - площадь треугольника.
3. Формула радиуса вписанной окружности через длины отрезков, проведенных из вершин треугольника в центр окружности:
Если из каждой вершины треугольника провести отрезок до центра окружности, то эти отрезки будут равными радиусу вписанной окружности. Формула в этом случае будет выглядеть следующим образом:
R = (a * b * c) / (4 * S),
где R - радиус вписанной окружности, a, b, c - длины отрезков, проведенных из вершин треугольника в центр окружности, S - площадь треугольника.
Используя одну из этих формул, можно найти радиус вписанного треугольника и использовать эту информацию в дальнейших расчетах и построениях.
Формула для расчета радиуса вписанного треугольника
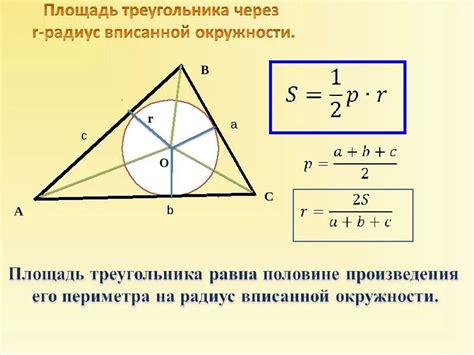
Формула для расчета радиуса вписанного треугольника:
| Стороны треугольника | Формула |
|---|---|
| a, b, c | r = a * b * c / (4 * S) |
Где:
- r - радиус вписанного треугольника;
- a, b, c - длины сторон треугольника;
- S - площадь треугольника.
Формула основана на связи радиуса вписанной окружности с площадью треугольника. Радиус можно выразить через стороны треугольника и площадь по данной формуле. Использование этой формулы позволяет легко и быстро определить радиус вписанного треугольника, зная его стороны.
Зачем нужно знать радиус вписанного треугольника

Знание радиуса вписанного треугольника имеет множество практических применений:
1. Вычисление площади и периметра треугольника.
С помощью радиуса вписанного треугольника можно легко вычислить его площадь и периметр. Для этого нужно знать длину каждой стороны треугольника и значение радиуса, которую можно получить из формулы радиуса окружности: радиус = площадь треугольника / полупериметр треугольника.
2. Решение геометрических задач.
Знание радиуса вписанного треугольника помогает решать большое количество геометрических задач. Например, можно использовать радиус для определения взаимного расположения двух треугольников или для доказательства равенства разных углов треугольника.
3. Конструирование фигур.
Радиус вписанного треугольника позволяет определить расстояние от центра окружности до каждой вершины треугольника. Эта информация полезна при конструировании различных геометрических фигур, таких как равносторонний треугольник или многоугольник.
В общем, знание радиуса вписанного треугольника расширяет возможности в изучении и решении геометрических задач, а также в конструировании фигур. Поэтому при изучении геометрии или применении ее в практических задачах полезно знать радиус вписанного треугольника.



