Описанная окружность равностороннего треугольника – это еще одна интересная и полезная концепция, связанная с геометрией треугольников. Определение и вычисление радиуса описанной окружности помогает нам лучше понять свойства и связи между его сторонами. В данной статье мы рассмотрим формулу для вычисления радиуса описанной окружности равностороннего треугольника и приведем несколько примеров для лучшего понимания.
Равносторонний треугольник - это треугольник, у которого все стороны равны друг другу, а все углы равны 60 градусам. Из-за своей симметрии равносторонний треугольник имеет некоторые уникальные свойства, которые его отличают от других типов треугольников. Одно из таких свойств - наличие описанной окружности, которая проходит через все вершины треугольника. Это основное свойство, которое определяет радиус описанной окружности равностороннего треугольника и делает его интересным объектом изучения.
Формула для расчета радиуса описанной окружности равностороннего треугольника может быть выведена, используя связь между радиусом окружности и длиной стороны треугольника. Учитывая, что радиус окружности является расстоянием от центра окружности до любой из вершин треугольника, можно установить соотношение между радиусом и длиной стороны. Получим следующую формулу:
R = a / √3
Где R - радиус описанной окружности, а a - длина стороны равностороннего треугольника. Эта формула позволяет нам легко вычислить радиус, зная длину стороны треугольника. Данную формулу можно использовать при решении задач и нахождении отдельных величин в равностороннем треугольнике.
Теория радиуса описанной окружности равностороннего треугольника
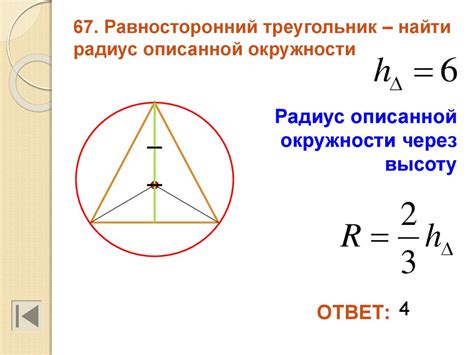
Радиус описанной окружности равностороннего треугольника равен половине стороны этого треугольника. Иными словами, если сторона равностороннего треугольника равна a, то его радиус описанной окружности равен a/2.
Это свойство может быть полезно при решении задач, связанных с равносторонним треугольником. Например, если известен радиус описанной окружности равностороннего треугольника, то можно легко найти его сторону, умножив радиус на 2.
Также, радиус описанной окружности равностороннего треугольника является основой для нахождения его площади. Площадь равностороннего треугольника можно найти по формуле: S = (a^2 * sqrt(3))/4, где a - сторона треугольника.
Зная радиус описанной окружности, можно также найти его центр, который является центром окружности. Для этого нужно провести перпендикуляр из середины одной стороны равностороннего треугольника к противоположной стороне. Точка пересечения этого перпендикуляра с описанной окружностью будет являться центром окружности.
Формула для расчета радиуса описанной окружности
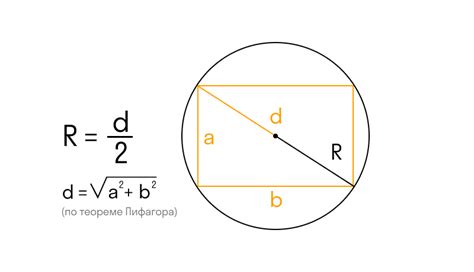
Радиус описанной окружности равностороннего треугольника может быть найден с помощью следующей формулы:
r = a / √3
где:
- r - радиус описанной окружности
- a - длина стороны равностороннего треугольника
Для использования данной формулы необходимо знать длину одной из сторон равностороннего треугольника. Если известна длина a, можно легко вычислить радиус описанной окружности, разделив длину стороны на корень из 3.
Например, пусть длина стороны равностороннего треугольника равна 6 единицам. Тогда радиус описанной окружности будет:
r = 6 / √3
r ≈ 3.46
Таким образом, радиус описанной окружности равностороннего треугольника с длиной стороны 6 единиц составляет около 3.46 единицы.
Примеры расчета радиуса описанной окружности:
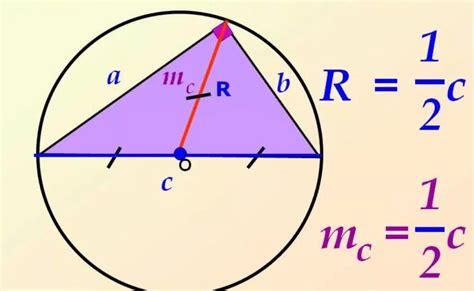
В данном случае, a = 6 см.
Радиус описанной окружности равностороннего треугольника будет: R = 6 / √3 ≈ 3.46 см.
2. Предположим, у нас есть равносторонний треугольник с радиусом описанной окружности равным 5 см. Для вычисления длины стороны треугольника воспользуемся обратной формулой: a = R * √3, где R - радиус описанной окружности.
В данном случае, R = 5 см.
Длина стороны равностороннего треугольника будет: a = 5 * √3 ≈ 8.66 см.
3. Пусть у нас есть равносторонний треугольник со стороной 10 см. Чтобы найти площадь треугольника, воспользуемся формулой: S = (a^2 * √3) / 4, где a - длина стороны треугольника.
В данном случае, a = 10 см.
Площадь равностороннего треугольника будет: S = (10^2 * √3) / 4 ≈ 43.3 см^2.



