Простые числа – это особенные числа, которые можно разделить только на 1 и на само себя. Они не имеют других делителей, кроме этих двух чисел. Простые числа являются важной темой в математике, и их изучение начинается уже в 5 классе.
Определить, что число является простым, можно с помощью различных методов. Первый способ заключается в проверке всех возможных делителей числа. Если число делится только на 1 и на само себя, то оно является простым.
Другой способ определения простого числа – использование решета Эратосфена. Этот метод позволяет найти все простые числа до заданного числа. Для этого нужно составить список всех чисел от 2 до данного числа и последовательно вычеркивать всех их кратных чисел. В результате останутся только простые числа.
Знание простых чисел позволяет решать различные задачи и задания, связанные с числами. Оно является фундаментом для изучения более сложных концепций в математике, таких как разложение на множители и нахождение наибольшего общего делителя.
Определение простых чисел
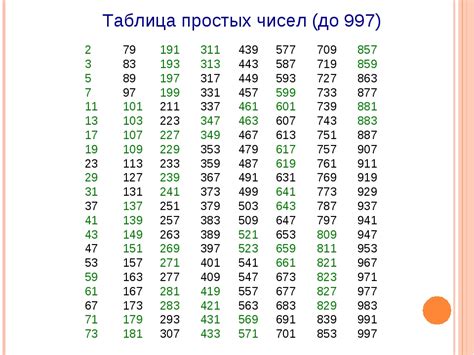
Например, числа 2, 3, 5, 7, 11 и 13 являются простыми числами, так как они имеют только два делителя - 1 и само число.
Определение простых чисел является важной темой в математике и находит много применений в различных областях, включая криптографию и теорию чисел.
Для определения, является ли число простым, можно использовать различные методы, такие как деление на все числа от 2 до квадратного корня из самого числа, проверка на делимость на предыдущие простые числа и т.д. Наиболее распространенным способом нахождения простых чисел является "Решето Эратосфена", когда изначально полагается, что все числа являются простыми, а затем последовательно исключаются числа, имеющие делители.
Способы нахождения простых чисел

Существует несколько способов нахождения простых чисел:
1. Перебор делителей:
Для каждого натурального числа можно перебрать все его делители и проверить, сколько из них являются простыми числами. Этот способ является очень простым и нужно иметь только базовые знания о делителях и простых числах.
2. Решето Эратосфена:
Решето Эратосфена – это алгоритм нахождения всех простых чисел до заданного числа. Он основан на принципе исключения: сначала все числа помечаются как простые, затем начинаются шаги, на каждом из которых отмечаются числа, кратные числу, которое является простым. В конце останутся только непомеченные числа, которые и являются простыми числами.
3. Проверка на делимость:
Еще один способ нахождения простых чисел – это проверка каждого числа на делимость на предшествующие числа. Если число делится без остатка только на 1 и на само себя, то оно является простым. Этот способ требует больше времени и ресурсов для нахождения простых чисел, но является универсальным и может применяться для любых числовых последовательностей.
Используя один из этих способов, можно легко находить простые числа и использовать их для решения различных задач и проблем.



