Определить принадлежность точки к плоскости - это одна из основных задач геометрии, которая применяется в различных областях науки и техники. В данной статье мы рассмотрим основные методы и примеры, которые помогут вам разобраться в этой проблеме.
Первый метод, который поможет определить принадлежность точки к плоскости, - это метод подстановки. Суть его заключается в том, что мы подставляем координаты точки в уравнение плоскости и проверяем, выполняется ли оно. Если выполняется, значит точка принадлежит плоскости, в противном случае точка не принадлежит плоскости. Этот метод является одним из самых простых и понятных.
Однако, существует и другой метод, который основан на геометрическом представлении плоскости и точки. Этот метод называется методом проекции. Суть его заключается в том, что мы проводим перпендикуляр из точки на плоскость и сравниваем его с нормалью плоскости. Если перпендикуляр и нормаль плоскости сонаправлены или параллельны, то точка принадлежит плоскости, в противном случае - не принадлежит.
В данной статье мы рассмотрели основные методы определения принадлежности точки к плоскости. Они позволяют с легкостью решить эту задачу в различных ситуациях. Теперь вы сможете применить эти методы на практике и уверенно решать геометрические задачи, связанные с плоскостью и точками.
Определение принадлежности точки к плоскости
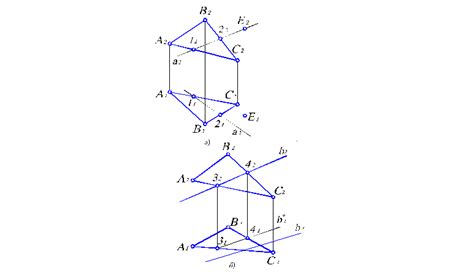
Существуют несколько методов, позволяющих определить принадлежность точки к плоскости.
1. Метод подстановки:
Суть метода заключается в подстановке координат точки в уравнение плоскости и проверке выполнения этого уравнения. Если результат равен нулю, то точка лежит на плоскости. Если результат больше нуля, то точка находится над плоскостью, а если результат меньше нуля, то точка находится под плоскостью.
2. Метод векторных проекций:
Для определения принадлежности точки к плоскости векторный метод использует вектор, параллельный плоскости и перемножение этого вектора на вектор, направленный от любой точки плоскости к исследуемой точке. Если результат равен нулю, то точка лежит на плоскости. Если результат больше нуля, то точка находится над плоскостью, а если результат меньше нуля, то точка находится под плоскостью.
3. Метод уравнения плоскости:
Уравнение плоскости, заданное в общем виде Ax + By + Cz + D = 0, позволяет определить принадлежность точки к плоскости путем подстановки координат точки в это уравнение и проверки выполнения равенства. Если результат равен нулю, то точка лежит на плоскости. Если результат больше нуля, то точка находится над плоскостью, а если результат меньше нуля, то точка находится под плоскостью.
Прежде чем приступить к определению принадлежности точки к плоскости, необходимо учесть параметры плоскости, такие как координаты точки на плоскости, нормаль плоскости и другие данный, необходимые для выбранного метода.
Четкое определение принадлежности точки к плоскости является важным шагом при решении многих задач геометрии и находит применение в различных областях человеческой деятельности.
Методы определения
1. Метод подстановки: Данный метод заключается в замене координат точек и плоскости в уравнение плоскости. Если равенство выполняется, то точка принадлежит плоскости.
2. Метод задания: В этом методе задается уравнение плоскости и координаты точки. Затем координаты точки подставляются в уравнение плоскости, и если равенство выполняется, то точка принадлежит плоскости.
3. Метод векторного произведения: Данный метод основан на векторном произведении векторов, определяющих плоскость и вектора, соединяющие точку с вершинами треугольника плоскости. Если все векторные произведения равны нулю, то точка принадлежит плоскости.
4. Метод использования нормали: В этом методе задается точка на плоскости и вектор нормали к плоскости. Затем находится скалярное произведение вектора, соединяющего заданную точку с точкой на плоскости, и вектора нормали. Если скалярное произведение равно нулю, то точка принадлежит плоскости.
Выбор метода определения принадлежности точки к плоскости зависит от конкретной задачи и доступных данных. Важно учитывать точность и эффективность каждого метода для получения правильного результата.
Примеры определения
Определение принадлежности точки к плоскости может быть полезным во многих областях, например, в компьютерной графике, анализе данных и геометрии. Вот несколько примеров, демонстрирующих различные методы определения:
| Метод | Пример |
|---|---|
| Использование уравнения плоскости | Пусть у нас есть плоскость с уравнением 3x + 2y - z = 6. Чтобы определить, принадлежит ли точка (1, 2, -1) этой плоскости, подставим координаты точки в уравнение: 3 * 1 + 2 * 2 - (-1) = 3 + 4 + 1 = 8 Так как результат не равен 6, то точка (1, 2, -1) не принадлежит плоскости. |
| Использование векторного произведения | Предположим, у нас есть плоскость, заданная точкой (1, 1, 1) и нормальным вектором (2, -1, 3). Чтобы определить, принадлежит ли точка (3, 1, 2) этой плоскости, найдем векторное произведение между векторами OA и AB, где O - точка плоскости, A - заданная точка плоскости, B - проверяемая точка: OA = (1, 1, 1) AB = (3, 1, 2) - (1, 1, 1) = (2, 0, 1) Теперь найдем векторное произведение: OA x AB = (1, 1, 1) x (2, 0, 1) = (1, -1, -2) Если векторное произведение равно нулевому вектору, то точка (3, 1, 2) принадлежит плоскости. В нашем случае, векторное произведение не равно нулевому вектору, поэтому точка не принадлежит плоскости. |
| Использование расстояния до плоскости | Пусть дана плоскость с уравнением 2x - y + 3z = 8 и точка (1, 2, 3). Чтобы определить, принадлежит ли точка плоскости, можно найти расстояние между точкой и плоскостью: Расстояние = |(2 * 1 - 2 + 3 * 3 - 8) / (sqrt(2^2 + (-1)^2 + 3^2))| Расстояние = |2 - 2 + 9 - 8| / sqrt(14) Расстояние = 1 / sqrt(14) Если расстояние равно нулю, то точка (1, 2, 3) принадлежит плоскости. В данном случае, расстояние не равно нулю, поэтому точка не принадлежит плоскости. |



